Question

已知x、y∈R,且满足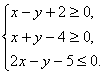求:

(1)t=x²+y²+2x-2y+2的最小值;

(2)t=|x+2y-4|的最大值;

(3)t=的范围.

Answer 1

解:在xOy坐标系内作出点(x,y)的平面区域如下图阴影部分.

(1)∵t=()²,

∴t可看成是平面区域内任一点(x,y)到点M(-1,1)的距离的平方.

∵直线x+y-4=0和直线x-y+2=0垂直,

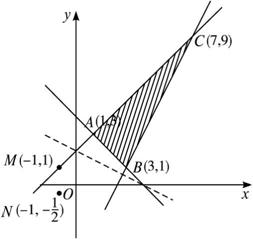
∴t的最小值即为M点到直线x+y-4=0的距离的平方,

    即t_min=()²=8.

(2)∵t=|x+2y-4|=·,

∴t可看成是平面区域内任一点(x,y)到直线x+2y-4=0的距离的倍.

    由图知,C点到直线x+2y-4=0的距离最大.

    由得C(7,9).

∴t_max=·=21.

(3)∵t==2×,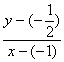

∴t可看成是平面区域内任一点(x,y)与点N(-1,-)连线的斜率的两倍.

    由得A(1,3).

    由得B(3,1).

∵k_NA==,k_NB==,∴t∈［,］.