题目内容
已知x,y∈R且x2+y2=1,a,b∈R为常数,t=
+
则( )
| a2x2+b2y2 |
| b2x2+a2y2 |
分析:直接利用不等式x+y≤
可求出t的最大值,令
=(ax,by),
=(bx,ay),利用t=
+
≥|
+
|可求最小值.
| 2(x2+y2) |
| m |
| n |
| |m| |
| |n| |
| m |
| n |
解答:解:t=
+
≤
=
当且仅当a2x2+b2y2=b2x2+a2y2时取等号
∴t有最大值
令
=(ax,by),
=(bx,ay)
则t=
+
=
+
≥|
+
|=
=|a+b|
∴t有最小值|a+b|
∴t有最大值也有最小值
故选A.
| a2x2+b2y2 |
| b2x2+a2y2 |
| 2(a2x2+b2y2+b2x2+a2y2) |
| 2(a2+b2) |
当且仅当a2x2+b2y2=b2x2+a2y2时取等号
∴t有最大值
| 2(a2+b2) |
令
| m |
| n |
则t=
| a2x2+b2y2 |
| b2x2+a2y2 |
| |m| |
| |n| |
| m |
| n |
| (ax+bx)2+(by+ay)2 |
∴t有最小值|a+b|
∴t有最大值也有最小值
故选A.
点评:本题主要考查了基本不等式,以及构造法的应用,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
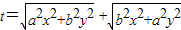 则( )
则( )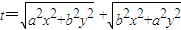 则( )
则( )