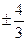题目内容
(本小题满分14分)
已知椭圆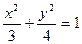 的焦点F与抛物线C:
的焦点F与抛物线C: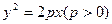 的焦点关于直线x-y=0
的焦点关于直线x-y=0
对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab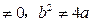 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,
BM与抛物线的另一交点为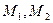 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要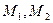 存在
存在
且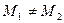 )直线
)直线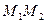 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.
已知椭圆
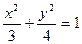 的焦点F与抛物线C:
的焦点F与抛物线C: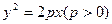 的焦点关于直线x-y=0
的焦点关于直线x-y=0对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab
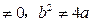 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,BM与抛物线的另一交点为
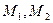 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要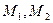 存在
存在且
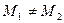 )直线
)直线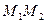 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.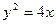 ,
,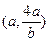
解:(Ⅰ)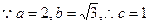 . …..1分
. …..1分
椭圆的焦点在y轴上,即F(0,1),F关于直线x-y=0对称的点为(1,0);…..2分
而抛物线的焦点坐标为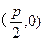 即得p=2,所以所求抛物线的方程为
即得p=2,所以所求抛物线的方程为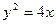 .…..5分
.…..5分
(Ⅱ)证明:设M,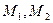 的坐标分别为
的坐标分别为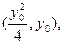
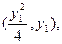
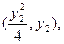
由A、M、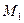 三点共线得:
三点共线得: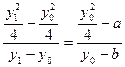 , …..7分
, …..7分
化简得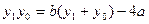 ,
,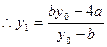 ;
;
同理,由B、M、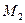 三点共线得:
三点共线得: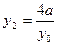 . …..9分
. …..9分
设(x,y)是直线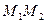 上的任意一点,则
上的任意一点,则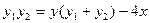 ;…..10分
;…..10分
把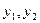 代入上式整理得:
代入上式整理得: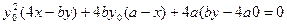 ;
;
由M是任意的,则有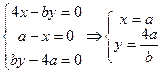 , …..13分
, …..13分
所以动直线 恒过定点
恒过定点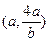 . …..14分
. …..14分
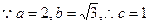 . …..1分
. …..1分椭圆的焦点在y轴上,即F(0,1),F关于直线x-y=0对称的点为(1,0);…..2分
而抛物线的焦点坐标为
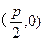 即得p=2,所以所求抛物线的方程为
即得p=2,所以所求抛物线的方程为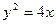 .…..5分
.…..5分(Ⅱ)证明:设M,
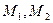 的坐标分别为
的坐标分别为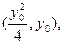
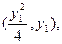
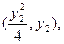
由A、M、
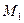 三点共线得:
三点共线得: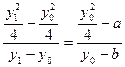 , …..7分
, …..7分化简得
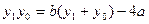 ,
,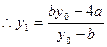 ;
;同理,由B、M、
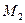 三点共线得:
三点共线得: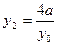 . …..9分
. …..9分设(x,y)是直线
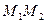 上的任意一点,则
上的任意一点,则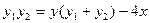 ;…..10分
;…..10分把
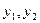 代入上式整理得:
代入上式整理得: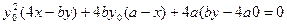 ;
;由M是任意的,则有
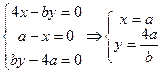 , …..13分
, …..13分所以动直线
 恒过定点
恒过定点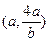 . …..14分
. …..14分
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
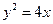 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.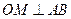 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;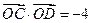 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.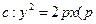 >0)上有两动点A、B(AB不垂直
>0)上有两动点A、B(AB不垂直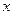 轴),F为焦点,且
轴),F为焦点,且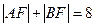 ,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
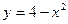 与直线
与直线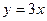 的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),
的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),
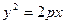 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则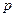 的值为( )
的值为( )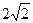
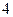
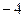
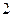
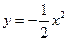 的焦点坐标是___ ,
的焦点坐标是___ ,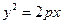 的焦点与椭圆
的焦点与椭圆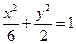 的右焦点重合,则
的右焦点重合,则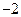 的值为( ﹡ )
的值为( ﹡ )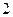
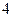
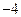
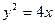 上的不同两点,F为抛物线C的焦点,若
上的不同两点,F为抛物线C的焦点,若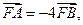 则直线AB的斜率为 ( )
则直线AB的斜率为 ( )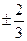 B.
B.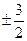 C.
C.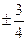 D.
D.