题目内容
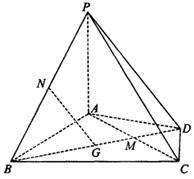
如图,在四棱锥P—ABCD中,ABCD为平行四边形,且BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2.
(Ⅰ)求证:PD//平面AMC;
(Ⅱ)若AB=1,求二面角B—AC—M的余弦值。
(Ⅰ)详见解析;(Ⅱ)二面角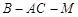 的余弦值为
的余弦值为 .
.
解析试题分析:(Ⅰ)要证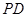 //平面
//平面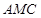 ,只需在平面
,只需在平面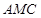 找一条直线与
找一条直线与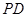 平行即可,证明线线平行,可利用三角形的中位线平行,也可利用平行四边形的对边平行,本题
平行即可,证明线线平行,可利用三角形的中位线平行,也可利用平行四边形的对边平行,本题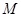 为
为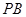 的中点,可考虑利用三角形的中位线平行,连接
的中点,可考虑利用三角形的中位线平行,连接 ,设
,设 与
与 相交于点
相交于点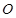 ,连接
,连接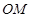 ,利用三角形中位线性质,证得
,利用三角形中位线性质,证得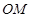 //
//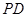 ,从而证明
,从而证明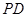 //平面
//平面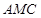 ;(Ⅱ)求二面角B—AC—M的余弦值,可找二面角的平面角,取
;(Ⅱ)求二面角B—AC—M的余弦值,可找二面角的平面角,取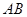 的中点
的中点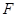 ,连接
,连接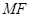 ,作
,作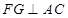 ,垂足为
,垂足为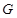 ,连接
,连接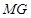 ,证明
,证明 为二面角
为二面角 的平面角,即可求得二面角
的平面角,即可求得二面角 的余弦值;也可利用空间坐标来求,以点
的余弦值;也可利用空间坐标来求,以点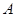 为坐标原点,分别以
为坐标原点,分别以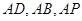 所在直线为
所在直线为 轴,
轴,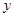 轴和
轴和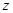 轴,建立空间直角坐标系
轴,建立空间直角坐标系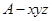 ,写出各点的坐标,由于
,写出各点的坐标,由于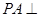 平面
平面 ,故平面
,故平面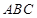 的一个法向量为
的一个法向量为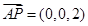 ,设出平面
,设出平面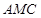 的法向量,通过
的法向量,通过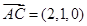 ,
,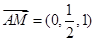 ,求出平面
,求出平面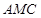 的法向量
的法向量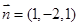 ,从而得二面角B—AC—M的余弦值.
,从而得二面角B—AC—M的余弦值.
试题解析:(Ⅰ)证明:?连接 ,设
,设 与
与 相交于点
相交于点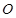 ,连接
,连接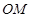 ,
,
????∵?四边形 是平行四边形,∴点
是平行四边形,∴点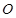 为
为 的中点.????????????????
的中点.????????????????
∵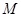 为
为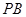 的中点,∴
的中点,∴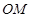 为
为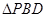 的中位线,
的中位线,
∴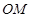 //
//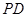 ,????????? 3分
,????????? 3分
∵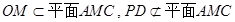 ,
,
∴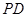 //
//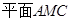 .???????? 6分
.???????? 6分
?(Ⅱ)??解法一?:?∵ 平面
平面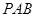 ,
,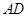 //
//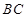 ,?则
,?则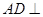 平面
平面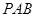 ,故
,故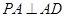 ,
,
又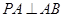 ??且
??且 ,
,
∴?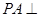 平面
平面 ,取
,取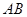 的中点
的中点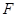 ,连接
,连接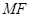 ,则
,则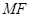 //
//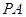 ,且?
,且?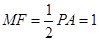 .∴?
.∴?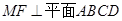 .
.
作
练习册系列答案
相关题目
 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,
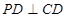 ,且
,且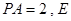 点满足
点满足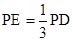 .
. 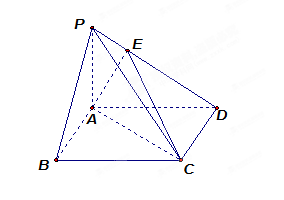
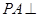 平面
平面 上是否存在点
上是否存在点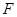 ,使得
,使得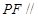 平面
平面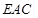 ?若存在,确定点
?若存在,确定点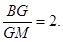
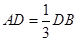 ,点C为圆O上一点,且
,点C为圆O上一点,且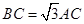 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.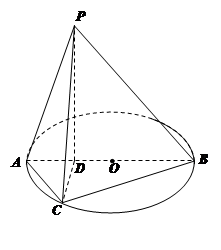
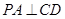 ;
;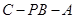 的余弦值.
的余弦值.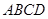 所在平面与圆
所在平面与圆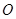 所在的平面相交于
所在的平面相交于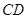 ,线段
,线段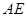 垂直于圆
垂直于圆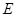 为圆
为圆 、
、 的点,设正方形
的点,设正方形 ,且
,且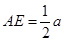 .
.
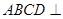 平面
平面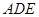 ;
;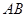 与
与 所成的角为
所成的角为 ,
,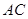 与底面
与底面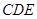 所成角为
所成角为 ,二面角
,二面角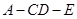 所成角为
所成角为 ,求证
,求证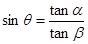
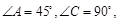
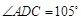 ,
,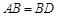 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD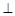 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

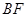 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值. 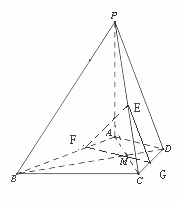
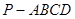 中,底面为直角梯形,
中,底面为直角梯形,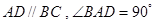 ,
,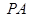 垂直于底面
垂直于底面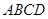 ,
,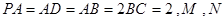 分别为
分别为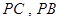 的中点.
的中点.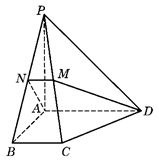
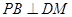 ;
;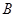 到平面
到平面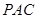 的距离.
的距离. 中,
中,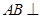 平面
平面 ,
,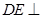 平面
平面
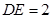 ,
,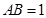 ,
,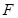 为
为 的中点.
的中点.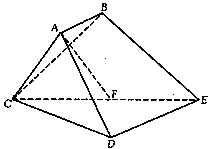
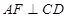 ;
;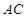 与平面
与平面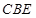 所成角的余弦值的大小.
所成角的余弦值的大小.