题目内容
已知定义在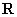 上的函数
上的函数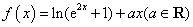 是偶函数.
是偶函数.
(1)求实数 的值;
的值;
(2)判断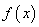 在
在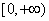 上的单调性,并用定义法证明;
上的单调性,并用定义法证明;
(3)若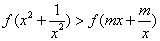 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解答】:(1)因为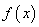 是定义在
是定义在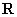 上的偶函数,所以
上的偶函数,所以 ,
,
即 ,即
,即 ,得
,得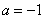 , ……………2分
, ……………2分
当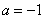 时,
时, ,
,
对于 ,综上
,综上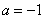 ………4分
………4分
(2)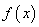 在
在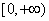 上是单调增函数, ………………………………5分
上是单调增函数, ………………………………5分
证明如下:
设 为
为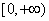 内的任意两个值,且
内的任意两个值,且 ,则
,则


因为 ,所以
,所以 ,所以
,所以 ,
,
所以 ,所以
,所以 ,
,
所以 ,所以
,所以 ,即
,即 ,
,
所以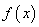 在
在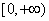 上是单调增函数. ………………………………10分
上是单调增函数. ………………………………10分
(3)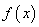 在
在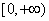 上是单调增函数,且是偶函数,又
上是单调增函数,且是偶函数,又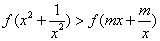 ,
,
所以 , ………………………………12分
, ………………………………12分
令 ,则
,则 ,
,
所以 ,
, 恒成立, ………………………………14分
恒成立, ………………………………14分
因为 ,关于
,关于 在
在 上单调递增,
上单调递增,
所以 ,所以
,所以 恒成立,所以
恒成立,所以 . ………………………16分
. ………………………16分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,若方程
,若方程 有三个根,求满足条件的实数k的取值是 .
有三个根,求满足条件的实数k的取值是 . ,若
,若 是
是 的充分不必要条件,则实数a的取值范围为 .
的充分不必要条件,则实数a的取值范围为 . 的方程
的方程 的两根为
的两根为 ,且满足
,且满足 ,则
,则 既是奇函数,又是周期函数,且周期为
既是奇函数,又是周期函数,且周期为 .当
.当 时,
时, (
( ),则
),则  的值为_________
的值为_________ 是“直线
是“直线 与圆
与圆 相交”的
相交”的 中,若
中,若 ,
, ,
, ,则边
,则边 __________.
__________. ·
·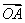 ≤0,
≤0,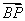 ·
· ≥0,则
≥0,则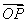 ·
·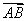 的最小值为________.
的最小值为________. 图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB、AC于不同的两点M、N,若
图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB、AC于不同的两点M、N,若 ,则m+n的值为________.
,则m+n的值为________.