题目内容
【题目】设椭圆C： 
的左焦点为F，过点F的直线与椭圆C相交于A，B两点，直线l的倾斜角为60°， 
． 
（1）求椭圆C的离心率；
（2）如果|AB|= 
，求椭圆C的方程．
【答案】
（1）解：设A（x1，y1），B（x2，y2），由题意知y1＞0，y2＜0
直线l的方程为 
，其中 
．
联立 
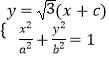得 
．
解得 
， 
．
因为 
，所以﹣y1=2y2．即﹣ 
=2 
，
解得离心率 
（2）解：因为 
，∴ 
．
由 
得 
，所以 
，解得a=3， 
．
故椭圆C的方程为 
．
【解析】（1）点斜式设出直线l的方程，代入椭圆，得到A、B的纵坐标，再由 ，求出离心率．（2）利用弦长公式和离心率的值，求出椭圆的长半轴、短半轴的值，从而写出标准方程．
【考点精析】本题主要考查了直线的倾斜角和椭圆的标准方程的相关知识点，需要掌握当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°；椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
练习册系列答案
相关题目
