Question

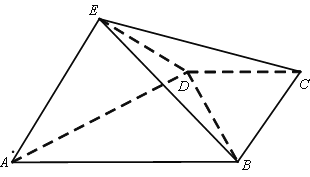
【题目】如图，在三棱锥中，平面平面， ，点在线段上，且， ，点在线段上，且.

（1）证明： 平面；

（2）若四棱锥的体积为7，求线段的长.

Answer 1

【答案】（1）见解析；（2）或.

【解析】试题分析：（Ⅰ）由等腰三角形的性质可证PE⊥AC，可证PE⊥AB．又EF∥BC，可证AB⊥EF，从而AB与平面PEF内两条相交直线PE，EF都垂直，可证AB⊥平面PEF．
（Ⅱ）设，可求AB，S△ABC，由EF∥BC可得△AFE∽△ABC，求得，由，可求S△AFD，从而求得四边形DFBC的面积，由（Ⅰ）知PE为四棱锥P-DFBC的高，求得PE，由体积，即可解得线段BC的长．

试题解析：

（1）证明：因为， ，所以点为等腰边的中点，所以.

又平面平面，平面平面， 平面， ，所以平面.

因为平面，所以.

因为， ，所以.

又因为平面， .

所以平面.

（2）解：设，则在中，

.

所以.

由， ，得，

故，即，

由， .

从而四边形的面积为 .

由（1）知平面，所以为四棱锥的高.

在中， .

所以

.

所以.

解得或.

由于，因此或.

所以或.