题目内容
11.已知O为四边形ABCD所在平面内的一点,若向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OD}$满足等式$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$+$\overrightarrow{OD}$,则四边形ABCD的形状是( )| A. | 平行四边形 | B. | 梯形 | C. | 三角形 | D. | 正方形 |
分析 如图所示,设AB,CD的中点分别为E,F点,利用平行四边形法则可得:$\overrightarrow{OA}+\overrightarrow{OB}$=2$\overrightarrow{OE}$,$\overrightarrow{OC}+\overrightarrow{OD}$=2$\overrightarrow{OF}$,由$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$+$\overrightarrow{OD}$,可得$\overrightarrow{OE}=\overrightarrow{OF}$,于是四边形ABCD是中心对称图形,即可得出.
解答 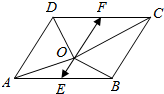 解:如图所示,
解:如图所示,
设AB,CD的中点分别为E,F点,
则$\overrightarrow{OA}+\overrightarrow{OB}$=2$\overrightarrow{OE}$,$\overrightarrow{OC}+\overrightarrow{OD}$=2$\overrightarrow{OF}$,
∵$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$+$\overrightarrow{OD}$,
∴$\overrightarrow{OE}=\overrightarrow{OF}$,
∴四边形ABCD是中心对称图形,
因此四边形ABCD是平行四边形.
故选:A.
点评 本题考查了向量平行四边形法则、中心对称图形的性质,考查了推理能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.已知函数f(x)=mx2+3(m-2)x-1在区间(-∞,3]上单调递减,则实数m的取值范围是( )
| A. | m<0 | B. | m=$\frac{2}{3}$ | C. | 0≤m≤$\frac{2}{3}$ | D. | m≥$\frac{2}{3}$ |
3.从4个男生,3个女生中挑选4人参加智力竞赛,要求至少有一个女生参加的选法共有( )
| A. | 12种 | B. | 34种 | C. | 35种 | D. | 36种 |
1.如果把两条平行的直线称为“一对”,那么在正方体的12条棱中,相互平行的直线共有( )对.
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |