题目内容
如图,四边形 是正方形,
是正方形,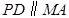 ,
,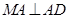 ,
,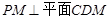 ,
, 
(Ⅰ)求证:平面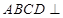 平面
平面 ;
;
(Ⅱ)求三棱锥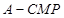 的高
的高
 是正方形,
是正方形, ,
, ,
,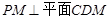 ,
, 
(Ⅰ)求证:平面
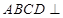 平面
平面 ;
;(Ⅱ)求三棱锥
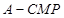 的高
的高 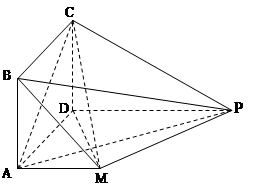
①见解析 ②

试题分析:(I)要证面面垂直,只要证明线面垂直,只要证明线线垂直:即找到直线
 (Ⅱ)因为
(Ⅱ)因为 ,所以求点面距离转化为等体积方法计算,容易求出三角形
,所以求点面距离转化为等体积方法计算,容易求出三角形 的面积与高
的面积与高 的值, 再计算出三角形
的值, 再计算出三角形 的面积即可
的面积即可 试题解析:(Ⅰ)

 平面
平面 ,且
,且 平面
平面 ,
,
 ,
,又
 是正方形,
是正方形,
 ,而梯形
,而梯形 中
中 与
与 相交,
相交, 平面
平面 ,
,又
 平面
平面 ,
, 平面
平面 平面
平面 4分
4分(Ⅱ)设三棱锥
 的高为
的高为 ,
,已证
 平面
平面 ,又
,又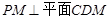 ,则
,则 ,
, ,
,由已知
 ,得
,得 ,
, ,
, , 6分
, 6分故
 ,
, 8分
8分

则
 10分
10分
 12分
12分故三棱锥
 的高为
的高为
(其他做法参照给分)

练习册系列答案
相关题目
 的底面
的底面 是平行四边形,且
是平行四边形,且 ,
, ,
,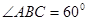 ,
,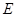 为
为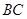 的中点,
的中点,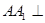 平面
平面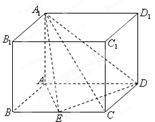
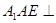 平面
平面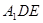 ;
;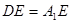 ,试求异面直线
,试求异面直线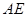 与
与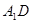 所成角的余弦值;
所成角的余弦值;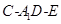 的余弦值.
的余弦值. 的直径,D为
的直径,D为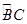 的中点,E为BC的中点.
的中点,E为BC的中点.
 的底面是边长为1的正六边形,
的底面是边长为1的正六边形, 底面
底面 。
。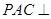 平面
平面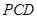 ;
;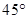 ,求三棱锥
,求三棱锥 高的大小。
高的大小。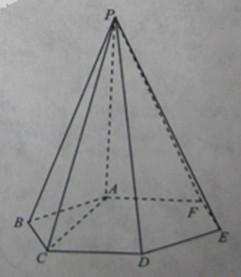
 中,AD//BC,
中,AD//BC, 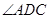 =900,BA="BC" 把ΔBAC沿
=900,BA="BC" 把ΔBAC沿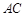 折起到
折起到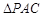 的位置,使得点
的位置,使得点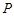 在平面ADC上的正投影O恰好落在线段
在平面ADC上的正投影O恰好落在线段 分别为线段PC,CD的中点.
分别为线段PC,CD的中点.
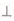 与平面POF;
与平面POF; ,使得
,使得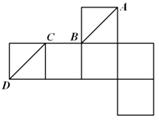
 B.
B.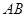 与
与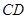 相交
相交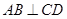 D.
D.
 是等腰直角三角形,其中
是等腰直角三角形,其中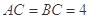 ,
,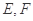 分别为
分别为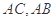 的中点,将
的中点,将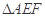 沿
沿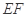 折起,点
折起,点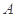 的位置变为点
的位置变为点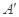 ,已知点
,已知点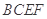 上的射影
上的射影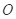 为
为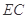 的中点,如图(2)所示.
的中点,如图(2)所示.
 ;
;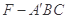 的体积.
的体积.