题目内容

以双曲线
x2
16
-
y2
9
=1的中心为顶点，左焦点为焦点的抛物线方程是
 
．
分析：利用双曲线的性质，结合题设条件求出抛物线的顶点坐标和焦点坐标，由此能求出抛物线方程．
解答：解：∵双曲线
x2
16
-
y2
9
=1的中心为（0，0），
左焦点为F（-5，0），
∴抛物线的顶点是（0，0），焦点坐标为F（-5，0），
设抛物线方程为y2=-2py，p＞0
则
p
2
=5，解得p=10，
∴抛物线方程为y2=-20x．
故答案为：y2=-20x．
点评：本题考查抛物线的方程的求法，解题时要熟练掌握双曲线和抛物线的性质，是基础题．
练习册系列答案
相关题目
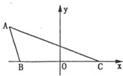精英家教网如图，△ABC外接圆半径R=
14
3
3
，∠ABC=120o，BC=10，弦BC在x轴上且y轴垂直平分BC边，则过点A且以B、C为焦点的双曲线的方程为（　　）
A、
x2
9
-
y2
16
=1
B、
x2
16
-
y2
9
=1
C、
x2
12
-
y2
13
=1
D、
x2
15
-
y2
10
=1
下列双曲线中，以y=±
1
2
x为渐近线的是（　　）
A、
x2
16
-
y2
4
=1
B、
x2
4
-
y2
16
=1
C、
x2
2
-y2=1
D、x2-
y2
2
=1
已知椭圆
x2
16
+
y2
9
=1与x轴交于A、B两点，焦点为F1、F2．
（1）求以F1、F2为顶点，以A、B为焦点的双曲线E的方程；
（2）M为双曲线E上一点，y轴上一点P (0，
16
3
)，求|MP|取最小值时M点的坐标．
分别以双曲线G：
x2
16
-
y2
9
=1的焦点为顶点，以双曲线G的顶点为焦点作椭圆C．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设点P的坐标为（0，3），在y轴上是否存在定点M，过点M且斜率为k的动直线l 交椭圆于A、B两点，使以AB为直径的圆恒过点P，若存在，求出M的坐标；若不存在，说明理由．
下列双曲线中，以y=±
1
2
x为渐近线的是（　　）
A．
x2
16
-
y2
4
=1		B．
x2
4
-
y2
16
=1		C．
x2
2
-y2=1		D．x2-
y2
2
=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网