题目内容

函数f（x）的图象与函数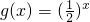 $数学公式$ 的图象关于直线y=x对称，则函数f（2x-x²）的单调递增区间是________．

[1，2）
分析：函数f（x）是g（x）= $\text{[math]}$ 的反函数，求出f（4-x²）的解析式，确定单调增区间．
解答：∵函数f（x）与g（x）= $\text{[math]}$ 的图象关于直线y=x对称，
∴函数f（x）是g（x）= $\text{[math]}$ 的反函数，∴f（x）= $\text{[math]}$ ，
f（2x-x²）= $\text{[math]}$ （2x-x²），
又2x-x²＞0，0＜x＜2，
t=2x-x²的对称轴为x=1，则其递减区间为[1，2）
∴f（4-x²）的增区间是[1，2）
故答案为：[1，2）
点评：本题考察反函数，函数的单调性和单调区间．关于反函数的求法，要会求一些简单函数的反函数，掌握互为反函数的函数图象间的关系．

练习册系列答案

中考导学案系列答案

中考大提速系列答案

中考专题通系列答案

中考第三轮复习冲刺专用模拟试卷系列答案

中考攻略中考及会考真题汇编系列答案

培优口算题卡系列答案

开心口算题卡系列答案

口算题卡河北少年儿童出版社系列答案

黄冈状元成才路口算题卡系列答案

趣味数学口算题卡系列答案

相关题目

已知函数f（x）=

，g（x）=-ax+1，其中a＞0．
（1）若函数f（x）的图象与函数g（x）的图象有公共点，且在公共点处有相同的切线，试求实数a的值；
（2）在区间（0，

]上至少存在一个实数x₀，使f（x₀）＞g（x₀）成立，试求实数a的取值范围．

已知二次函数f（x）=ax²+bx+c．
（1）若a＞b＞c且f（1）=0，判断函数f（x）的图象与x轴公共点的个数；
（2）证明：若对x₁，x₂且x₁＜x₂，f（x₁）≠f（x₂），则方程f（x）=

必有一实根在区间（x₁，x₂）内；
（3）在（1）的条件下，设f（x）=0的另一根为x₀，若方程f（x）+a=0有解证明-2＜x₀≤-1．

设函数f（x）=x³-12x，则下列结论正确的是（　　）

A．函数f（x）在（-∞，-1）上单调递增

B．函数f（x）的极小值是-12

C．函数f（x）的图象与直线y=10只有一个公共点

D．函数f（x）的图象在点（-2，f（-2））处的切线方程为y=16

（2012•安徽模拟）已知函数f（x）的图象与函数h(x)=x+

+2的图象关于点A（0，1）对称，则当x∈[

，2]时，f（x）的值域为（　　）

D．[2，+∞）

已知定义在[1，+∞）上的函数f(x)=

当x∈[2^n-1，2ⁿ]（n∈N^*）时，函数f（x）的图象与x轴围成的图形面积为S，则S=（　　）