题目内容
【题目】【选做题】本题包括A、B、C、D四小题，请选定其中两小题，并在相应的答题区域内作答．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．
（1）A．【选修4—1几何证明选讲】
如图，在△ABC中，∠ABC=90°，BD⊥AC ， D为垂足，E是BC的中点，求证：∠EDC=∠ABD.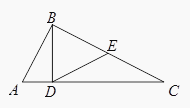
（2）B.【选修4—2：矩阵与变换】
已知矩阵A= 
矩阵B的逆矩阵B﹣1= 
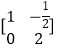，求矩阵AB.
（3）【选修4—4：坐标系与参数方程】在平面直角坐标系xOy中，已知直线l的参数方程为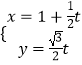 
（t为参数），椭圆C的参数方程为 
（ 
为参数）.设直线l与椭圆C相交于A ， B两点，求线段AB的长.
（4）D. 设a＞0，|x﹣1|＜ 
，|y﹣2|＜ ，求证：|2x+y﹣4|＜a．
【答案】
（1）
解：由 
可得 
，
由 
是 
中点可得 
，
则 
，
由 可得 
，
由 
可得 
，
因此 
，
又 可得 
（2）
解： 
，因此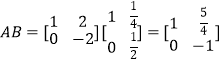 
．
（3）
解：直线 
方程化为普通方程为 
，
椭圆 
方程化为普通方程为 
，
联立得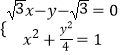 
，解得 
或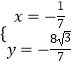 
，
因此 
（4）
证明：由 
可得 
，
【解析】A、依题意，知∠BDC=90°，∠EDC=∠C，利用∠C+∠DBC=∠ABD+∠DBC=90°，可得∠ABD=∠C，从而可证得结论．
B、依题意，利用矩阵变换求得B=（B﹣1）﹣1= 
= 
，再利用矩阵乘法的性质可求得答案．
C、分别化直线与椭圆的参数方程为普通方程，然后联立方程组，求出直线与椭圆的交点坐标，代入两点间的距离公式求得答案．
D、运用绝对值不等式的性质：|a+b|≤|a|+|b|，结合不等式的基本性质，即可得证．
【考点精析】解答此题的关键在于理解直线的参数方程的相关知识，掌握经过点
，倾斜角为
的直线
的参数方程可表示为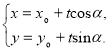
（
为参数），以及对椭圆的参数方程的理解，了解椭圆
的参数方程可表示为
．
