题目内容
已知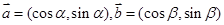 则 ( )
则 ( )
A.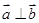 | B.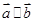 |
C.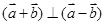 | D.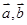 的夹角为 的夹角为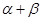 |
C
解析试题分析:根据题意由于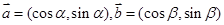 ,则可知
,则可知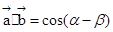 ,而对于
,而对于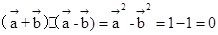 ,从而说明向量
,从而说明向量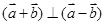 成立,对于D,
成立,对于D,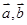 的夹角为
的夹角为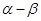 ,故错误,对于B,由于向量的坐标不符合共线的公式,故错误,选C.
,故错误,对于B,由于向量的坐标不符合共线的公式,故错误,选C.
考点:向量的数量积
点评:主要是考查了向量的数量积的坐标运算属于基础题

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案已知向量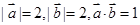 ,则向量
,则向量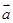 与
与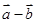 的夹角为( )
的夹角为( )
A.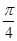 | B.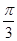 | C.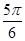 | D.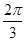 |
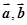 是两个向量,
是两个向量,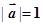 ,
,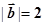 ,且
,且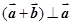 ,则
,则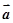 与
与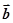 的夹角为( )
的夹角为( )
A.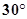 | B. | C.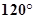 | D.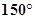 |
已知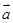 、
、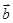 是平面向量,若
是平面向量,若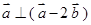 ,
,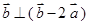 ,则
,则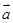 与
与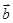 的夹角是( )
的夹角是( )
A.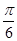 | B.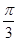 | C.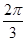 | D.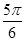 |
在ΔABC中,已知D是AB边上一点,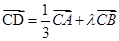 ,则实数λ=
,则实数λ=
A.-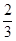 | B.-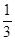 | C.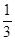 | D.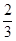 |
若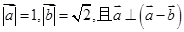 ,则向量
,则向量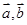 的夹角为
的夹角为
| A.45° | B.60° | C.120° | D.135° |
已知向量 ,
, 满足|
满足| |="2," |
|="2," |  |=l,且(
|=l,且( +
+ )⊥(
)⊥(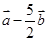 ),则
),则 与
与 的夹角为
的夹角为
A.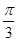 | B.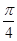 | C.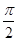 | D.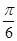 |
已知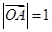 ,
,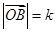 ,
,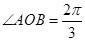 ,点C在
,点C在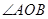 内,
内, 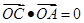 ,若
,若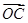 =2m
=2m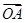 +m
+m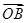 (
(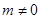 ),则
),则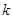 =( )
=( )
| A.1 | B.2 | C.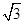 | D.4 |
 的边长为
的边长为 ,
,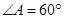 ,
, 为
为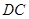 的中点,则
的中点,则 的值为 .
的值为 .