题目内容
(12分)是否存在自然数 ,使得f (n) = (2n+7)·3n+ 9对于任意
,使得f (n) = (2n+7)·3n+ 9对于任意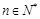 都能被
都能被 整除,若存在,求出
整除,若存在,求出 (如果m不唯一,只求m的最大值);若不存在,请说明理由。
(如果m不唯一,只求m的最大值);若不存在,请说明理由。
【答案】
命题对于一切自然数n(n∈N)均成立。
【解析】解  .猜想
.猜想 的值应为其最大公约数36.
的值应为其最大公约数36.
①  显然正确.
显然正确.
② 设n=k时命题正确,即f (k) = (2k+7)·3k+ 9 能被36整除.
则 时 ,
时 ,
 能被36整除,
能被36整除,
即n=k+1时,命题正确。
综合上述,命题对于一切自然数n(n∈N)均成立。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
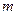 ,使得f (n) = (2n+7)·3n+ 9对于任意
,使得f (n) = (2n+7)·3n+ 9对于任意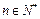 都能被
都能被 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为 ,
, .
. 是
是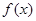 的导函数,且
的导函数,且
 );
); 满足
满足 ,且
,且 ,求数列
,求数列 ,
, ,是否存在自然数
,是否存在自然数 ,使得当
,使得当 时
时
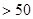 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的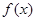 是二次函数,不等式
是二次函数,不等式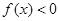 的解集是
的解集是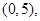 且
且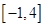 上的最大值是12.
上的最大值是12.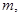 使得方程
使得方程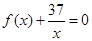 在区间
在区间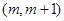 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出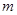 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.