题目内容
已知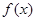 是二次函数,不等式
是二次函数,不等式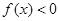 的解集是
的解集是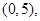 且
且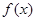 在区间
在区间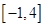 上的最大值是12.
上的最大值是12.
(Ⅰ)求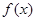 的解析式;
的解析式;
(Ⅱ)是否存在自然数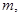 使得方程
使得方程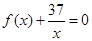 在区间
在区间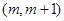 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出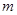 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
【答案】
(I)
(II)存在惟一的自然数 使得方程
使得方程 在区间
在区间 内有且只有两个不同的实数根.
内有且只有两个不同的实数根.
【解析】(I) 是二次函数,且
是二次函数,且 的解集是
的解集是 可设
可设
因为f(x)的对称轴为 ,所以可确定
,所以可确定 在区间
在区间 上的最大值是
上的最大值是 据此可得到关于a的方程,从而得到f(x)的解析式.
据此可得到关于a的方程,从而得到f(x)的解析式.
(II) 方程 等价于方程
等价于方程 设
设
然后再根据导数研究h(x)的单调性和极值,最值画出其草图从图上分析解决即可.
(I)
 是二次函数,且
是二次函数,且 的解集是
的解集是
 可设
可设
 在区间
在区间 上的最大值是
上的最大值是
由已知,得
 (4分)
(4分)
(II)方程 等价于方程
等价于方程
设 则
则
当 时,
时, 是减函数;
是减函数;
当 时,
时, 是增函数.(8分)
是增函数.(8分)

 方程
方程 在区间
在区间 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间
 内没有实数根. (11分)
内没有实数根. (11分)
所以存在惟一的自然数 使得方程
使得方程 在区间
在区间 内有且只有两个不同的实数根.(13分)
内有且只有两个不同的实数根.(13分)

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且 上的最大值是12.
上的最大值是12. 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实
内有且只有两个不等的实 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.








 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且 上的最大值是12.
上的最大值是12. 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实
内有且只有两个不等的实 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且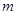 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出