Question

一货轮航行到M处，测得灯塔S在货轮的北偏东15°相距20里处，随后货轮按北偏西30°的方向航行，半小时后，又测得灯塔在货轮的北偏东60°处，则货轮的航行速度为________里/小时．

Answer 1

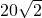
分析：设货轮按北偏西30°的方向航行，半小时后到达N，航行的速度为x由题意可得，MS=20，MN=，∠SMN=45°，∠S=45°，∠SNM=90°，MN=NS=x，MS=20，在 Rt△MNS中求解即可
解答：设货轮按北偏西30°的方向航行，半小时后到达N，航行的速度为x
由题意可得，MS=20，MN=，∠SMN=45°，∠S=45°，∠SNM=90°，
MN=NS=x，MS=20，由勾股定理可得x=20
故答案为：20
MN
点评：本题主要考查了解三角形在事件问题中的应用，关键问题是要把题中所给的方位角转化为数学问题中三角形的角度，进而选择合适的公式进行求解．