题目内容
给出三个结论:
(1)0一定是奇函数的零点;
(2)偶函数一定有偶数个零点;
(3)周期函数一定有无穷多个零点.
(4)单调函数至多有一个零点.
其中正确的结论个数为______.
解:四个结论:
(1)如对于函数y= ,它是奇函数,故0不一定是奇函数的零点;错误.
,它是奇函数,故0不一定是奇函数的零点;错误.
(2)偶函数的图象关于y轴对称,故其零点一定有偶数个零点;正确.
(3)如对于函数y=sinx+2,它是周期函数,但其没有零点,故周期函数不一定有无穷多个零点.错误.
(4)单调函数的图象是上升的或下降的,故其与x轴的至多有一个交点,故单调函数至多有一个零点.正确.
其中正确的结论个数为2.
故答案为:2.
分析:通过举反例可得出结论(1)、(3)不一定正确,利用单调函数性质对(2)进行判断,利用单调函数性质对(4)进行判断.
点评:本题考查函数的零点,正确解答本题,关键是理解4个命题所涉及的函数的性质及图象的特征,将零点个数问题转化为函数图象与横轴交点个数问题也很关键.
(1)如对于函数y=
 ,它是奇函数,故0不一定是奇函数的零点;错误.
,它是奇函数,故0不一定是奇函数的零点;错误.(2)偶函数的图象关于y轴对称,故其零点一定有偶数个零点;正确.
(3)如对于函数y=sinx+2,它是周期函数,但其没有零点,故周期函数不一定有无穷多个零点.错误.
(4)单调函数的图象是上升的或下降的,故其与x轴的至多有一个交点,故单调函数至多有一个零点.正确.
其中正确的结论个数为2.
故答案为:2.
分析:通过举反例可得出结论(1)、(3)不一定正确,利用单调函数性质对(2)进行判断,利用单调函数性质对(4)进行判断.
点评:本题考查函数的零点,正确解答本题,关键是理解4个命题所涉及的函数的性质及图象的特征,将零点个数问题转化为函数图象与横轴交点个数问题也很关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
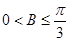 ;(2)
;(2)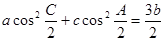 ;(3)
;(3)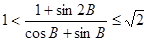 。
。 ;
; ;
; .
.