题目内容

已知A（3，y），B（-5，2），C（6，-9）三点共线，则y=
-6
-6
．
分析：由A（3，y），B（-5，2），C（6，-9）三点共线，可得kAB=kBC，利用斜率计算公式即可得出．
解答：解：∵A（3，y），B（-5，2），C（6，-9）三点共线，
∴kAB=kBC，
∴
2-y
-5-3
=
-9-2
6-(-5)
，化为2-y=8，解得y=-6．
故答案为-6．
点评：本题考查了三点共线与斜率之间的关系，属于基础题．
练习册系列答案
相关题目
已知A（3，1），B（-1，2），若∠ACB的平分线在y=x+1上，则AC所在直线方程是（　　）
已知A（3，-2），B（-5，4），则以AB为直径的圆的方程是（　　）
（2008•宁波模拟）已知A（3，2），B（5，5），C（0，4），动点P（x，y）在△ABC内部或边界上，则定点Q（5，0）到点P（x，y）的最小距离为
2
2
 latex=“
2
“＞2 latex=“
2
 latex=“
2
“＞2“＞2
2
2
 latex=“
2
“＞2 latex=“
2
 latex=“
2
“＞2“＞2
．
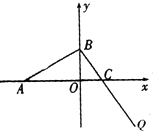精英家教网如图，已知A（-3，0），B、C两点分别在y轴和x轴上运动，并且满足
AB
•
BQ
=0，
BC
=
1
2
CQ
．
（1）求动点Q的轨迹方程；
（2）设过点A的直线与Q的轨迹交于E、F两点，A′（3，0），求直线A′E、A′F的斜率之和．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网