题目内容
在△ABC中,点G为中线AD上一点,且AG=| 1 | 2 |
分析:如图所示,利用向量的运算法则可得
=
-
=(
-m)
+
.
=
-
=
+(
-n)
.再利用向量共线定理可得,存在实数t使得
=t
,利用向量相等即可得出:
+
=4.再利用基本不等式即可得出m+3n的最小值.
| MG |
| AG |
| AM |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| NG |
| AG |
| AN |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| MG |
| NG |
| 1 |
| m |
| 1 |
| n |
解答:解:如图所示,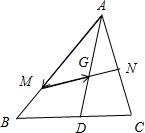
=
-
=
-m
=
×
(
+
)-m
=(
-m)
+
.
=
-
=
-n
=
×
(
+
)-n
=
+(
-n)
.
∵
与
共线,∴存在实数t,使得
=t
,
∴(
-m)
+
=t[
+(
-n)
],
∴
-m=
t,
=t(
-n),
消去t可得:
+
=4.
∵m>0,n>0,
∴m+3n=
(
+
)(m+3n)=
(4+
+
)≥
(4+2
)=2+
,
当且仅当m=
n=
时取等号.
因此m+3n的最小值为
+1.
故答案为:
+1.

| MG |
| AG |
| AM |
| 1 |
| 2 |
| AD |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
| AB |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| NG |
| AG |
| AN |
| 1 |
| 2 |
| AD |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
| AC |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
∵
| MG |
| NG |
| MG |
| NG |
∴(
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
∴
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
消去t可得:
| 1 |
| m |
| 1 |
| n |
∵m>0,n>0,
∴m+3n=
| 1 |
| 4 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 4 |
| m |
| n |
| 3n |
| m |
| 1 |
| 4 |
|
| ||
| 2 |
当且仅当m=
| 3 |
| ||
| 4 |
因此m+3n的最小值为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题综合考查了向量的运算法则、向量共线定理、向量相等、基本不等式等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
 选考题
选考题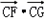 的取值范围.
的取值范围. 的取值范围.
的取值范围.