题目内容
已知在矩形ABCD中,AB=5,BC=7,在其中任取一点P,使满足∠APB>90°,则P点出现的概率为
.
| 5π |
| 56 |
| 5π |
| 56 |
分析:在矩形ABCD内以AB为直径作半圆,如图所示.由直径所对的圆周角为直角,可得当点P位于半圆内部满足∠APB>90°.因此,算出半圆的面积和矩形ABCD的面积,利用几何概型公式加以计算,即可得到P点出现的概率.
解答: 解:在矩形ABCD内,以AB为直径作半圆,如图所示.
解:在矩形ABCD内,以AB为直径作半圆,如图所示.
∵P点在半圆上时,∠APB=90°,
∴当点P位于半圆内部满足∠APB>90°.
∵矩形ABCD中,AB=5,BC=7,∴矩形ABCD的面积S=AB×BC=35.
又∵半圆的面积S'=
×π×(
)2=
,
∴点P出现的概率为P=
=
=
.
故答案为:
 解:在矩形ABCD内,以AB为直径作半圆,如图所示.
解:在矩形ABCD内,以AB为直径作半圆,如图所示.∵P点在半圆上时,∠APB=90°,
∴当点P位于半圆内部满足∠APB>90°.
∵矩形ABCD中,AB=5,BC=7,∴矩形ABCD的面积S=AB×BC=35.
又∵半圆的面积S'=
| 1 |
| 2 |
| AB |
| 2 |
| 25π |
| 8 |
∴点P出现的概率为P=
| S′ |
| S |
| ||
| 35 |
| 5π |
| 56 |
故答案为:
| 5π |
| 56 |
点评:本题给出矩形ABCD,求矩形内部一点P满足∠APB>90°的概率.着重考查了半圆、矩形的面积公式和几何概型计算公式等知识,属于基础题.

练习册系列答案
相关题目
已知在矩形ABCD中,AB=2,BC=3,则
+
+
的模等于( )
| AB |
| BC |
| AC |
| A、4 | ||
| B、5 | ||
C、
| ||
D、2
|
 ,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1.
,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1.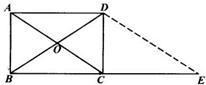 如图所示,已知在矩形ABCD中,
如图所示,已知在矩形ABCD中, (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题: