题目内容
过点A(-4,0)向椭圆| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求ab最大时椭圆的方程;
(Ⅱ)对(Ⅰ)中的椭圆,若其左焦点为F,过F的直线l与y轴交于点M,与椭圆的一个交点为Q,且|
| MQ |
| QF |
分析:(Ⅰ)由题意,其中一条切线的方程为:y=
(x+4),联立方程组
,消去y得3b2x2+a2((x+4)2=3a2b2,由△=0,可得a2+3b2=16,0<ab≤
,当a2=3b2时,ab取最大值,求得a2=8,b2=
,由此能求出椭圆的方程.
(Ⅱ)由F(-
,0),设直线方程为:y=k(x+
),设Q(x0,y0),则M(0,
k),当
=2
时,有定比分点公式可得:x0=-
,y0=
k.由此能求出直线方程.
| ||
| 3 |
|
8
| ||
| 3 |
| 8 |
| 3 |
(Ⅱ)由F(-
4
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
| MQ |
| QF |
8
| ||
| 9 |
4
| ||
| 9 |
解答:解:(Ⅰ)由题意,其中一条切线的方程为:y=
(x+4)(2分)
联立方程组
消去y得3b2x2+a2((x+4)2=3a2b2
即(a2+3b2)x2+8a2x+16a2-3a2b2=0有△=0,可得a2+3b2=16
因为a2+3b2=16,所以16≥2
,即0<ab≤
(4分)
所以当a2=3b2时,ab取最大值;求得a2=8,b2=
故椭圆的方程为
+
=1(6分)
(Ⅱ)由(Ⅰ)知,F(-
,0),设直线方程为:y=k(x+
)
设Q(x0,y0),则M(0,
k)当
=2
时,有定比分点公式可得:x0=-
,y0=
k(8分)
代入椭圆解得k=±
直线方程为y=±
(x+
)(10分)
同理当
=-2
时,16k2=-
无解
故直线方程为y=±
(x+
)(12分)
| ||
| 3 |
联立方程组
|
即(a2+3b2)x2+8a2x+16a2-3a2b2=0有△=0,可得a2+3b2=16
因为a2+3b2=16,所以16≥2
| 3a2b2 |
8
| ||
| 3 |
所以当a2=3b2时,ab取最大值;求得a2=8,b2=
| 8 |
| 3 |
故椭圆的方程为
| x2 |
| 8 |
| 3y2 |
| 8 |
(Ⅱ)由(Ⅰ)知,F(-
4
| ||
| 3 |
4
| ||
| 3 |
设Q(x0,y0),则M(0,
4
| ||
| 3 |
| MQ |
| QF |
8
| ||
| 9 |
4
| ||
| 9 |
代入椭圆解得k=±
| ||
| 6 |
| ||
| 6 |
4
| ||
| 3 |
同理当
| MQ |
| QF |
| 40 |
| 3 |
故直线方程为y=±
| ||
| 6 |
4
| ||
| 3 |
点评:本题考查求ab最大时椭圆的方程和求直线方程,解题时要认真审题,仔细解答,注意培养计算能力.

练习册系列答案
相关题目
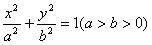 引两条切线,切点分别为B,C,且△ABC为正三角形。
引两条切线,切点分别为B,C,且△ABC为正三角形。 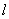 与y轴交于点M,与椭圆的一个交点为Q,且
与y轴交于点M,与椭圆的一个交点为Q,且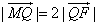 ,求直线
,求直线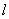 的方程。
的方程。 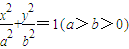 引两条切线,切点分别为B,C,且△ABC为正三角形.
引两条切线,切点分别为B,C,且△ABC为正三角形.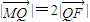 ,求直线l的方程.
,求直线l的方程.