题目内容
过点A(-4,0)向椭圆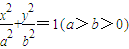 引两条切线,切点分别为B,C,且△ABC为正三角形.
引两条切线,切点分别为B,C,且△ABC为正三角形.(Ⅰ)求ab最大时椭圆的方程;
(Ⅱ)对(Ⅰ)中的椭圆,若其左焦点为F,过F的直线l与y轴交于点M,与椭圆的一个交点为Q,且
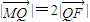 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(Ⅰ)由题意,其中一条切线的方程为: ,联立方程组
,联立方程组 ,消去y得3b2x2+a2((x+4)2=3a2b2,由△=0,可得a2+3b2=16,
,消去y得3b2x2+a2((x+4)2=3a2b2,由△=0,可得a2+3b2=16,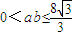 ,当a2=3b2时,ab取最大值,求得
,当a2=3b2时,ab取最大值,求得 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.
(Ⅱ)由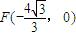 ,设直线方程为:
,设直线方程为: ,设Q(x,y),则
,设Q(x,y),则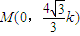 ,当
,当 时,有定比分点公式可得:
时,有定比分点公式可得: .由此能求出直线方程.
.由此能求出直线方程.
解答:解:(Ⅰ)由题意,其中一条切线的方程为: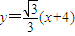 (2分)
(2分)
联立方程组 消去y得3b2x2+a2((x+4)2=3a2b2
消去y得3b2x2+a2((x+4)2=3a2b2
即(a2+3b2)x2+8a2x+16a2-3a2b2=0有△=0,可得a2+3b2=16
因为a2+3b2=16,所以 ,即
,即 (4分)
(4分)
所以当a2=3b2时,ab取最大值;求得
故椭圆的方程为 (6分)
(6分)
(Ⅱ)由(Ⅰ)知, ,设直线方程为:
,设直线方程为:
设Q(x,y),则 当
当 时,有定比分点公式可得:
时,有定比分点公式可得: (8分)
(8分)
代入椭圆解得 直线方程为
直线方程为 (10分)
(10分)
同理当 时,
时, 无解
无解
故直线方程为 (12分)
(12分)
点评:本题考查求ab最大时椭圆的方程和求直线方程,解题时要认真审题,仔细解答,注意培养计算能力.
 ,联立方程组
,联立方程组 ,消去y得3b2x2+a2((x+4)2=3a2b2,由△=0,可得a2+3b2=16,
,消去y得3b2x2+a2((x+4)2=3a2b2,由△=0,可得a2+3b2=16,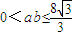 ,当a2=3b2时,ab取最大值,求得
,当a2=3b2时,ab取最大值,求得 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.(Ⅱ)由
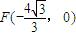 ,设直线方程为:
,设直线方程为: ,设Q(x,y),则
,设Q(x,y),则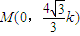 ,当
,当 时,有定比分点公式可得:
时,有定比分点公式可得: .由此能求出直线方程.
.由此能求出直线方程.解答:解:(Ⅰ)由题意,其中一条切线的方程为:
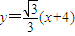 (2分)
(2分)联立方程组
 消去y得3b2x2+a2((x+4)2=3a2b2
消去y得3b2x2+a2((x+4)2=3a2b2即(a2+3b2)x2+8a2x+16a2-3a2b2=0有△=0,可得a2+3b2=16
因为a2+3b2=16,所以
 ,即
,即 (4分)
(4分)所以当a2=3b2时,ab取最大值;求得

故椭圆的方程为
 (6分)
(6分)(Ⅱ)由(Ⅰ)知,
 ,设直线方程为:
,设直线方程为:
设Q(x,y),则
 当
当 时,有定比分点公式可得:
时,有定比分点公式可得: (8分)
(8分)代入椭圆解得
 直线方程为
直线方程为 (10分)
(10分)同理当
 时,
时, 无解
无解故直线方程为
 (12分)
(12分)点评:本题考查求ab最大时椭圆的方程和求直线方程,解题时要认真审题,仔细解答,注意培养计算能力.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
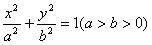 引两条切线,切点分别为B,C,且△ABC为正三角形。
引两条切线,切点分别为B,C,且△ABC为正三角形。 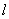 与y轴交于点M,与椭圆的一个交点为Q,且
与y轴交于点M,与椭圆的一个交点为Q,且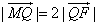 ,求直线
,求直线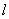 的方程。
的方程。