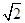题目内容
已知
是椭圆
上的一动点，且与椭圆长轴两顶点连线的斜率之积最小值为
，则椭圆离心率为
A． | B． | C． | D． |
B
解析试题分析：由题意可知P位于短轴顶点处满足斜率乘积为，
考点：椭圆的离心率
点评：求离心率关键是找到关于
的齐次方程或不等式
练习册系列答案
阅读快车系列答案
相关题目
双曲线的离心率为
，则双曲线的两条渐近线的夹角是
| A．45° | B．30° | C．60° | D．90° |
若抛物线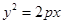
的焦点与椭圆
的右焦点重合，则
的值为( )
| A．-2 | B．2 | C．-4 | D．4 |
过椭圆
的右焦点F2作倾斜角为
弦AB，则|AB︳为（ ）
A． | B． | C． | D． |
如图，椭圆
的四个顶点
构成的四边形为菱形，若菱形
的内切圆恰好过焦点，则椭圆的离心率是
A． | B． | C． | D． |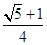
+
=1的两焦点，经点F2的直线交椭圆于点A、B，若|AB|=5，则|AF1|+|BF1|等于（ ）与椭圆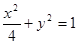
共焦点且过点
的双曲线方程是（ ）
A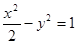． | B． |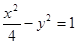
C． | D． |
等轴双曲线C的中心在原点，焦点在
轴上，C与抛物线
的准线交于A,B两点，
,则C的实轴长为（ ）
| A．2 | B． | C．4 | D． |
