题目内容
过椭圆 的右焦点F2作倾斜角为
的右焦点F2作倾斜角为 弦AB,则|AB︳为( )
弦AB,则|AB︳为( )
A. | B. | C. | D. |
B
解析试题分析:椭圆 ,则a=
,则a= ,b=1, c=1,
,b=1, c=1, ,两个焦点
,两个焦点 (-1,0),
(-1,0),  (1,0)。
(1,0)。
直线AB的方程为y=x-1 ,代入 整理得3
整理得3
所以由弦长公式得|AB|= =
= ,故选B.
,故选B.
考点:本题主要考查直线与椭圆的位置关系,弦长公式的应用。
点评:基础题,利用数形结合思想,通过确定弦的方程,进一步转化成代数问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知曲线 (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为 ,若P为其上一点,
,若P为其上一点,  , 则双曲线离心率的取值范围为( )
, 则双曲线离心率的取值范围为( )
A.(3,+ ) ) | B. | C.(1,3) | D.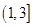 |
直线 与双曲线
与双曲线 仅有一个公共点,则实数
仅有一个公共点,则实数 的值为
的值为
| A.1 | B.-1 | C.1或-1 | D.1或-1或0 |
以 为中心,
为中心, ,
, 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点 ,满足
,满足 ,则该椭圆的离心率为
,则该椭圆的离心率为
A.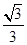 | B. | C. | D. |
过点 ,且与
,且与 有相同渐近线的双曲线方程是
有相同渐近线的双曲线方程是
A.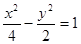 | B. |
C. | D. |
已知 是椭圆
是椭圆 上的一动点,且
上的一动点,且 与椭圆长轴两顶点连线的斜率之积最小值为
与椭圆长轴两顶点连线的斜率之积最小值为 ,则椭圆离心率为
,则椭圆离心率为
A. | B. | C. | D. |
已知点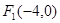 和
和 ,曲线上的动点P到
,曲线上的动点P到 、
、 的距离之差为6,则曲线方程为()
的距离之差为6,则曲线方程为()
A. | B.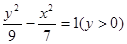 |
C. 或 或 | D. |
已知实数x、y满足2x+y+5=0,那么 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
点P到点 ,
, 及到直线
及到直线 的距离都相等,如果这样的点恰好只有一个,那么a的值是( )
的距离都相等,如果这样的点恰好只有一个,那么a的值是( )
A. | B. | C. 或 或 | D. 或 或 |