Question

【题目】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各面中，面积最大的是（ ）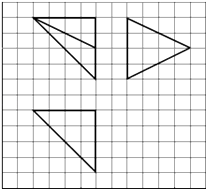
A.8
B.
C.12
D.16

Answer 1

【答案】C
【解析】解：根据题意，得； 该几何体是如图所示的三棱锥A﹣BCD，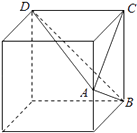

且该三棱锥是放在棱长为4的正方体中，
所以，在三棱锥A﹣BCD中，BD=4 ，AC=AB= = ，AD= =6，
S△ABC= ×4×4=8．S△ADC= =4 ，S△DBC= ×4×4=8，在三角形ABC中，作CE⊥ E，连结DE，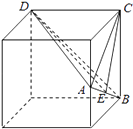

则CE= = ，DE= = ，
S△ABD= =12．
故选：C．
【考点精析】认真审题，首先需要了解由三视图求面积、体积(求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积)．