题目内容
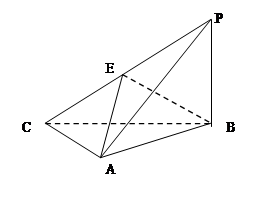
如图,三棱锥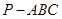 中,
中,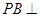 平面
平面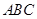 ,
,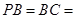
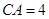 ,
,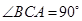 ,
,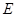 为
为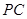 中点.
中点.
(1)求证: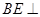 平面
平面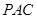 ;
;
(2)求二面角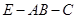 的正弦值.
的正弦值.
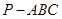 中,
中,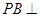 平面
平面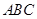 ,
,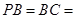
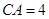 ,
,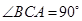 ,
,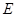 为
为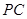 中点.
中点.
(1)求证:
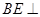 平面
平面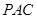 ;
;(2)求二面角
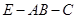 的正弦值.
的正弦值.(1)详见解析;(2)二面角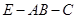 的正弦值为
的正弦值为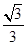 .
.
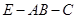 的正弦值为
的正弦值为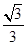 .
.试题分析:(1)要证直线
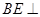 平面
平面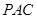 ,只需证
,只需证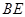 垂直于平面
垂直于平面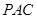 内的两条相交直线,首先在等腰三角形中利用三线合一的原理得到
内的两条相交直线,首先在等腰三角形中利用三线合一的原理得到 ,通过证明
,通过证明 平面
平面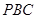 ,得到
,得到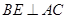 ,再结合直线与平面垂直的判定定理证明
,再结合直线与平面垂直的判定定理证明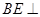 平面
平面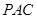 ;(2)解法一是利用三垂线法来求二面角
;(2)解法一是利用三垂线法来求二面角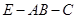 的正弦值,利用
的正弦值,利用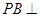 平面
平面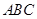 ,从点
,从点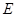 作
作 的中位线
的中位线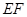 ,得到
,得到 平面
平面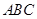 ,再过点
,再过点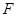 作
作 ,并连接
,并连接 ,先利用直线
,先利用直线 平面
平面 来说明
来说明 为二面角
为二面角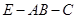 的平面角,最后在直角三角形
的平面角,最后在直角三角形 中来计算
中来计算 的正弦值;解法二是以点
的正弦值;解法二是以点 为原点,
为原点, 、
、 的方向分别为
的方向分别为 轴、
轴、 轴的正方向建立空间直角坐标系,利用空间向量法来求二面角
轴的正方向建立空间直角坐标系,利用空间向量法来求二面角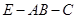 的余弦值,进而求出它的正弦值.
的余弦值,进而求出它的正弦值.试题解析:(1)
 平面
平面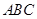 ,
, 平面
平面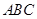 ,
,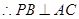 ,
, ,
,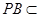 平面
平面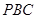 ,
, 平面
平面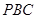 ,
, ,
, 平面
平面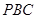 ,
,又
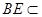 平面
平面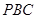 ,
,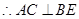 ,
, ,
,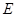 为
为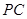 的中点,
的中点, ,
, 平面
平面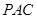 ,
,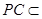 平面
平面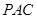 ,
, ,
,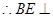 平面
平面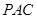 ;
;(2)方法一:取
 的中点
的中点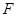 ,连接
,连接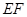 ,则
,则 .
.由已知得
 面
面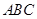 ,过
,过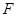 作
作 ,
,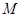 为垂足,连接
为垂足,连接 ,
,由(1)知,
 平面
平面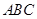 ,
, 平面
平面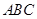 ,
, ,
, ,且
,且 ,
, 面
面 ,
,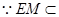 平面
平面 ,
, ,故
,故 为二面角
为二面角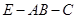 的平面角,
的平面角,
 ,
,故二面角
 的余弦值为
的余弦值为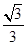 ;
;
方法二:以
 为原点建立空间直角坐标系B
为原点建立空间直角坐标系B ,
,
 ,
, ,
, ,
, ,
,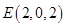 ,则
,则 ,
,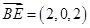 ,
,平面
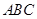 法向量为
法向量为 ,
,设平面
 法向量为
法向量为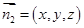 ,
,则

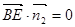
 .
.令z=1,得x=-1,y=1,.即
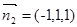 ,
,设二面角E-AB-C为
 ,则
,则 =
=
故二面角
 的余弦值为
的余弦值为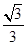 .
.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
 的底面
的底面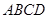 是平行四边形,且
是平行四边形,且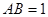 ,
,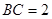 ,
,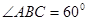 ,
,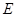 为
为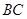 的中点,
的中点,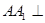 平面
平面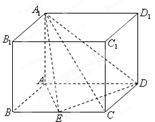
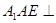 平面
平面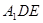 ;
;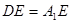 ,试求异面直线
,试求异面直线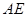 与
与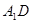 所成角的余弦值;
所成角的余弦值;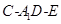 的余弦值.
的余弦值.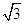 的球面上.若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上.若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.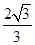 ,则它的外接球的表面积为( )
,则它的外接球的表面积为( )



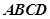 的棱长为1,M为AC的中点,P在线段DM上,则
的棱长为1,M为AC的中点,P在线段DM上,则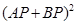 的最小值为_____________;
的最小值为_____________;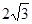 ,则三棱锥A-BCD的外接球的大圆面积为( )
,则三棱锥A-BCD的外接球的大圆面积为( )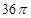
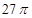

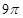
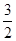 ,EF与面AC的距离为2,则该多面体的体积为____________.
,EF与面AC的距离为2,则该多面体的体积为____________.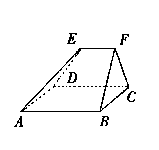
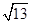 ,AB⊥平面ACD,则四面体 ABCD外接球的表面积为( )
,AB⊥平面ACD,则四面体 ABCD外接球的表面积为( )