题目内容
在二项式(2x-
)6的展开式中,含x2项的系数是 .
| 1 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于2,求得r的值,即可求得展开式中的含x2项的系数.
解答:
解:二项式(2x-
)6的展开式的通项公式为Tr+1=
•26-r•(-1)r•x6-2r,
令6-2r=2,r=2,∴含x2项的系数是
•24=240,
故答案为:240.
| 1 |
| x |
| C | r 6 |
令6-2r=2,r=2,∴含x2项的系数是
| C | 2 6 |
故答案为:240.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
一条线段夹在一个直二面角角的两个半平面内,它与两个半平面所成的角都是30°,则这条线段与这个二面角的棱所成角的大小为( )
| A、45° |
| B、45°或135° |
| C、60°或120° |
| D、30° |
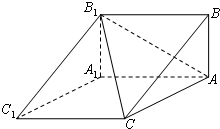 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2