题目内容
设G是△ABC的重心（即三条中线的交点），
=
，
=
．试用
•
表示
=
+
+
．
| AB |
| a |
| AC |
| b |
| a |
| b |
| AG |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
分析：由三角形的重心的性质，可得
=
，再结合向量的加法法则，化简得到结果．
| AG |
| 2 |
| 3 |
| AD |
解答：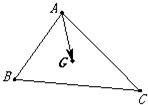
解：延长AG交BC于点D，由三角形的重心的定义可得D是BC的中点，再由三角形的重心的性质可得，
=
=
×
（
+
）
=
（
+
）
=
+
．
故答案为：
+
．
解：延长AG交BC于点D，由三角形的重心的定义可得D是BC的中点，再由三角形的重心的性质可得，| AG |
| 2 |
| 3 |
| AD |
=
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
=
| 1 |
| 3 |
| AB |
| AC |
=
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
故答案为：
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
点评：本题考查三角形的重心的性质，平面向量基本定理，属于基础题．
练习册系列答案
相关题目
设G是△ABC的重心，且(56sinA)
+(40sinB)
+(35sinC)
=
，则B的大小为（ ）
| GA |
| GB |
| GC |
| 0 |
| A、15° | B、30° |
| C、45° | D、60° |
设G是△ABC的重心，且(sinA)•
+(sinB)•
+(sinC)•
=
，则B的大小为（ ）
| GA |
| GB |
| GC |
| 0 |
| A、45° | B、60° |
| C、30° | D、15° |