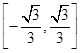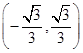题目内容
如图,圆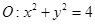 与坐标轴交于点
与坐标轴交于点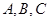 .
.
⑴求与直线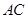 垂直的圆的切线方程;
垂直的圆的切线方程;
⑵设点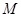 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线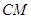 交
交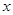 轴于点
轴于点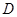 ,直线
,直线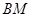 交直线
交直线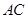 于点
于点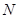 ,
,
①若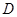 点坐标为
点坐标为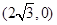 ,求弦
,求弦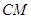 的长;②求证:
的长;②求证: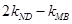 为定值.
为定值.
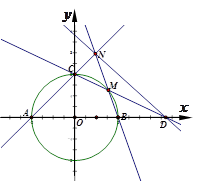
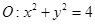 与坐标轴交于点
与坐标轴交于点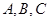 .
.⑴求与直线
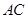 垂直的圆的切线方程;
垂直的圆的切线方程;⑵设点
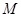 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线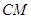 交
交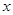 轴于点
轴于点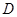 ,直线
,直线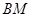 交直线
交直线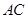 于点
于点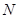 ,
,①若
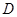 点坐标为
点坐标为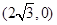 ,求弦
,求弦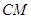 的长;②求证:
的长;②求证: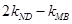 为定值.
为定值.
(1)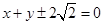 ,(2)①:2,②:证明略.
,(2)①:2,②:证明略.
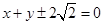 ,(2)①:2,②:证明略.
,(2)①:2,②:证明略.试题分析:(1)所求直线与
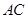 垂直,则斜率为负倒数关系,因此可依
垂直,则斜率为负倒数关系,因此可依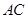 方程设出所求直线方程,利用圆心到此直线的距离为半径可求出此直线方程;(2)①为常考点,利用弦心距,半径,弦长的一半三者构成勾股定理的关系求解;②设直线
方程设出所求直线方程,利用圆心到此直线的距离为半径可求出此直线方程;(2)①为常考点,利用弦心距,半径,弦长的一半三者构成勾股定理的关系求解;②设直线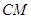 的方程为:
的方程为: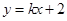 ,把
,把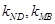 转化为含
转化为含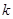 的代数式进行运算,也可设
的代数式进行运算,也可设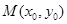 ,把
,把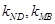 转化为含
转化为含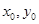 的代数式进行运算.
的代数式进行运算.试题解析:
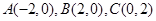 ,直线
,直线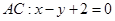 ,⑴设所求切线方程为
,⑴设所求切线方程为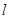 :
: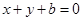 ,
,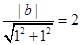 则
则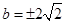 ,所以
,所以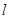 :
: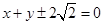 ;
;⑵①
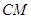 :
: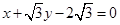 ,圆心到直线
,圆心到直线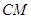 的距离
的距离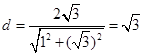 ,所以弦
,所以弦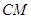 的长为
的长为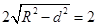 ;(或由等边三角形
;(或由等边三角形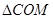 亦可).
亦可).②解法一:设直线
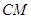 的方程为:
的方程为: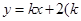 存在,
存在,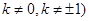 ,则
,则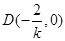
由
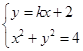 ,得
,得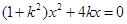 ,所以
,所以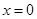 或
或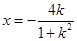 ,将
,将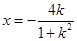 代入直线
代入直线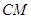 ,得
,得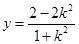 ,即
,即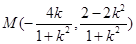 ,则
,则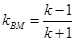 ,
,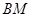 :
: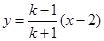 ,
,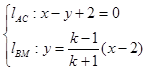 ,
,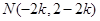 ,得
,得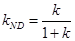 ,所以
,所以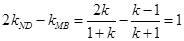 为定值.
为定值.解法二:设
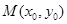 ,则
,则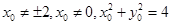 ,直线
,直线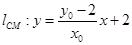 ,则
,则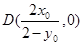 ,
,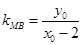 ,直线
,直线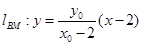 ,又
,又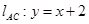 ,
,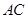 与
与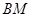 交点
交点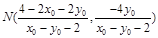 ,
,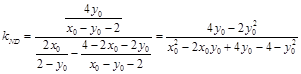 ,将
,将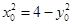 ,代入得
,代入得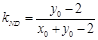 ,所以
,所以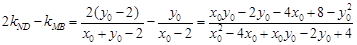 ,得
,得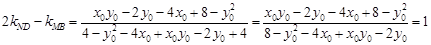 为定值.
为定值.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 的方程为
的方程为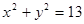 ,直线
,直线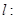
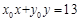 ,设点
,设点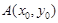 .
.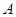 在圆
在圆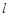 与圆
与圆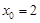 ,
,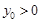 ,过点
,过点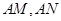 分别交圆
分别交圆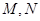 两点,且直线
两点,且直线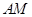 和
和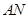 的斜率互为相反数;
的斜率互为相反数; 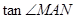 的值;
的值;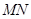 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.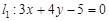 ,圆
,圆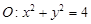 .
.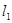 被圆
被圆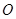 所截得的弦长;
所截得的弦长;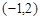 的直线
的直线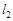 与直线
与直线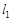 垂直,
垂直,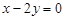 上的圆
上的圆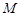 相切,圆
相切,圆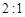 ,求圆
,求圆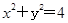 ,过点M(2,4)作圆C的两条切线,切点分别为A,B,
,过点M(2,4)作圆C的两条切线,切点分别为A,B,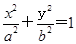 (a>b>0)的右顶点和上顶点.
(a>b>0)的右顶点和上顶点.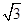 (k>0)与椭圆T相交于P,Q两点,O为坐标原点,
(k>0)与椭圆T相交于P,Q两点,O为坐标原点,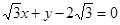 与圆
与圆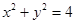 的位置关系是 (填相交、相切、相离)
的位置关系是 (填相交、相切、相离)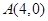 的直线
的直线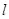 与曲线
与曲线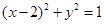 有公共点,则直线
有公共点,则直线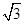 ,
,