题目内容
已知公差不为0的等差数列{an}的首项a1=3,设数列的前项和为Sn,且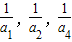 成等比数列.
成等比数列.(Ⅰ)求数列{an}的通项公式及Sn;
(II)求
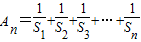 .
.
【答案】分析:(Ⅰ)依题意可求得等差数列{an}的公差,从而可数列{an}的通项公式及Sn;
(II)由(Ⅰ)里用裂项法可求得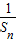 ,累加即可求得An.
,累加即可求得An.
解答:解:(Ⅰ)由a1=3且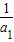 、
、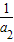 、
、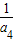 成等比数列得
成等比数列得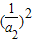 =
=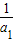 ×
×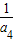 ,
,
即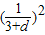 =
= ×
×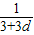 ,
,
解得d=3.
∴数列{an}的通项公式an=3n,
∴Sn=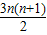 .
.
(2)∵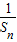 =
= (
(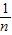 -
-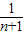 ),
),
∴An=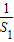 +
+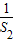 +…+
+…+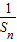 =
= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(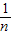 -
-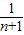 )]
)]
= (1-
(1-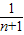 )
)
=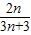 .
.
点评:本题考查等比数列的性质与裂项法求和,求得an的通项公式是关键,考查分析与转化的解决问题的能力,属于中档题.
(II)由(Ⅰ)里用裂项法可求得
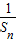 ,累加即可求得An.
,累加即可求得An.解答:解:(Ⅰ)由a1=3且
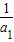 、
、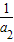 、
、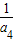 成等比数列得
成等比数列得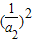 =
=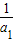 ×
×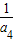 ,
,即
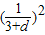 =
= ×
×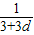 ,
,解得d=3.
∴数列{an}的通项公式an=3n,
∴Sn=
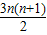 .
.(2)∵
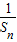 =
= (
(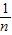 -
-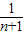 ),
),∴An=
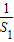 +
+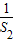 +…+
+…+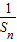 =
= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(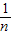 -
-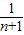 )]
)]=
 (1-
(1-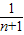 )
)=
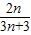 .
.点评:本题考查等比数列的性质与裂项法求和,求得an的通项公式是关键,考查分析与转化的解决问题的能力,属于中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目