题目内容
(2012•黄州区模拟)已知公差不为0的等差数列{an}的前3项和S3=9,且a1,a2,a5成等比数列.
(1)求数列{an}的通项公式和前n项和Sn
(2)设Tn为数列{
}的前n项和,若Tn≤λan+1对一切n∈N*恒成立,求实数λ的最小值.
(1)求数列{an}的通项公式和前n项和Sn
(2)设Tn为数列{
| 1 | anan+1 |
分析:(1)由等差数列的求和公式可得a1+d=3,由a1,a2,a5成等比数列,可得a1(a1+4d)=(a1+d)2,从而可求a1,d,从而可求
(2)由
=
=
(
-
),利用裂项可求数列的和Tn,然后由Tn≤λan+1得λ≥
=
,只要求
的最大值即可求出λ的范围
(2)由
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| (2n+1)2 |
| 1 | ||
4n+
|
| 1 | ||
4n+
|
解答:解:(1)由S3=9,可得3a1+3d=9即a1+d=3①(2分)
∵a1,a2,a5成等比数列.
∴a1(a1+4d)=(a1+d)2②;
联立①②得a1=1,d=2;…(4分)
故an=2n-1,Sn=n2…(6分)
(2)∵
=
=
(
-
)…(8分)
∴Tn=
(1-
+
-
+…+
-
)=
…(10分)
由Tn≤λan+1得:
≤λ(2n+1)
∴λ≥
=
令f(n)=
,
∵f(n)单调递增,
∴f(n)≤
即λ≥
…(12分)
∵a1,a2,a5成等比数列.
∴a1(a1+4d)=(a1+d)2②;
联立①②得a1=1,d=2;…(4分)
故an=2n-1,Sn=n2…(6分)
(2)∵
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
由Tn≤λan+1得:
| n |
| 2n+1 |
∴λ≥
| n |
| (2n+1)2 |
| 1 | ||
4n+
|
令f(n)=
| 1 | ||
4n+
|
∵f(n)单调递增,
∴f(n)≤
| 1 |
| 9 |
即λ≥
| 1 |
| 9 |
点评:本题考查的重点是数列的通项与求和,解题的关键是利用等差数列与等比数列的定义,利用裂项法求和.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
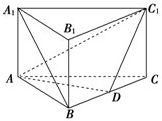 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为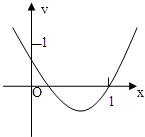 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )