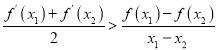Question

【题目】某同学对函数进行研究后，得出以下结论，其中正确的有（ ）

A.函数的图象关于原点对称

B.对定义域中的任意实数的值，恒有成立

C.函数的图象与轴有无穷多个交点，且每相邻两交点间距离相等

D.对任意常数，存在常数，使函数在上单调递减，且

Answer 1

【答案】BD

【解析】

由函数奇偶性定义判断可知A错误，由函数性质可知，构造函数，求导判断单调性，进而求得最值可知B正确，由的图象与轴的交点坐标为可判断C错误，求导分析时成立的情况，即可判断D选项.

对于A项：

函数的定义域为，

为偶函数，图象关于轴对称. 故A错误

对于B选项：

由A项知为偶函数，当时，

令，

，

在上单调递增. ，即恒成立 . 故B正确

对于C项：

函数的图象与轴的交点坐标为

交点与间的距离为，而其余任意相邻两点之间的距离为. 故C错误.

对于D项：

，

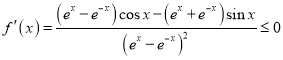即，即.

当时，，，区间长度为对于任意常数，存在常数，

使在上单调递减且.

故选：BD