题目内容
已知 展开式中的前三项系数成等差数列.
展开式中的前三项系数成等差数列.
(1)求n的值;
(2)求展开式中的常数项.
解:(1)∵ 展开式中的前三项系数
展开式中的前三项系数 ,
, ,
, 成等差数列,
成等差数列,
∴2× =
= +
+ ,即n2-9n+8=0,
,即n2-9n+8=0,
∴n=8或n=1(舍去),
∴n=8;
(2)∵ 展开式的通项公式Tr+1=
展开式的通项公式Tr+1= •
• •
• •
• =
= •
• •
• ,
,
∴要使Tr+1项为常数项,则8-2r=0,
∴r=4,
∴常数项为:T5=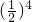 •
• =
=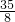 .
.
分析:(1)由于 展开式中的前三项系数为:
展开式中的前三项系数为: ,
, ,
, ,这三数成等差数列?2×
,这三数成等差数列?2× =
= +
+ ,从而可求得n;
,从而可求得n;
(2)由(1)求得n=8,利用 展开式的通项公式Tr+1=
展开式的通项公式Tr+1= •
• •
• •
• =
= •
• •
• ,由
,由 =0求得r,从而可求得展开式中的常数项.
=0求得r,从而可求得展开式中的常数项.
点评:本题考查二项式定理的应用与等差数列的性质,关键是掌握好二项展开式的通项公式,属于中档题.
 展开式中的前三项系数
展开式中的前三项系数 ,
, ,
, 成等差数列,
成等差数列,∴2×
 =
= +
+ ,即n2-9n+8=0,
,即n2-9n+8=0,∴n=8或n=1(舍去),
∴n=8;
(2)∵
 展开式的通项公式Tr+1=
展开式的通项公式Tr+1= •
• •
• •
• =
= •
• •
• ,
,∴要使Tr+1项为常数项,则8-2r=0,
∴r=4,
∴常数项为:T5=
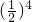 •
• =
=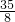 .
.分析:(1)由于
 展开式中的前三项系数为:
展开式中的前三项系数为: ,
, ,
, ,这三数成等差数列?2×
,这三数成等差数列?2× =
= +
+ ,从而可求得n;
,从而可求得n;(2)由(1)求得n=8,利用
 展开式的通项公式Tr+1=
展开式的通项公式Tr+1= •
• •
• •
• =
= •
• •
• ,由
,由 =0求得r,从而可求得展开式中的常数项.
=0求得r,从而可求得展开式中的常数项.点评:本题考查二项式定理的应用与等差数列的性质,关键是掌握好二项展开式的通项公式,属于中档题.

练习册系列答案
相关题目
 展开式中的前三项系数成等差数列.
展开式中的前三项系数成等差数列.