Question

已知某地每单位面积菜地年平均使用氮肥量xkg与每单位面积蔬菜年平均产量yt之间的关系有如下数据：

年份	1985	1986	1987	1988	1989	1990	1991	1992
x(kg)	70	74	80	78	85	92	90	95
y(t)	5.1	6.0	6.8	7.8	9.0	10.2	10.0	12.0
x(kg)	92	108	115	123	130	138	145
y(t)	11.5	11.0	11.8	12.2	12.5	12.8	13.0

    （1）画出散点图，并判断它们是否有相关关系;

    （2）若线性相关，求蔬菜产量y与使用氮肥量之间的回归直线方程，并估计每单位面积施肥150kg时，每单位面积蔬菜的年平均产量。

   

Answer 1

思路解析：画出散点图后，再判断是否具有相关关系。求回归直线方程，只需代入公式即可。

    答案：（1）散点图为：

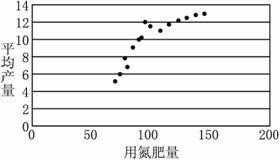
    因为所有的点都大致分布在一条直线的附近，所以它们具有相关关系。

（2）设所求的回归直线方程为=bx+a，则

b=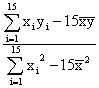=≈0.0937，

a=-b=10.11-0.0937×101≈0.6463，

∴回归直线方程为=0.0937x+0.6463

所以=0.0937×150+0.6463=14.701（t）。