题目内容
已知F(1,0),P是平面上一动点,P到直线l:x=-1上的射影为点N,且满足(| PN |
| 1 |
| 2 |
| NF |
| NF |
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过点M(1,2)作曲线C的两条弦MD,ME,且MD,ME所在直线的斜率为k1,k2,满足k1k2=1,
求证:直线DE过定点,并求出这个定点.
分析:(1)设曲线C上任意一点P(x,y),又F(1,0),N(-1,y),从而
=(-1-x,0),
=(2,-y),由此能得到所求的P点的轨迹C的方程.
(2)由题意可知直线DE的斜率存在且不为零,可设DE的方程为x=my+a,并设D(x1,y1),E(x2,y2).联立:
,代入整理得y2-4my-4a=0,再由韦达定理进行求解.
| PN |
| NF |
(2)由题意可知直线DE的斜率存在且不为零,可设DE的方程为x=my+a,并设D(x1,y1),E(x2,y2).联立:
|
解答:解:(1)设曲线C上任意一点P(x,y),又F(1,0),N(-1,y),从而
=(-1-x,0),
=(2,-y),
+
=(-x,-
y),(
+
)•
=0?-2x+
y2=0
化简得y2=4x,即为所求的P点的轨迹C的对应的方程.
(2)由题意可知直线DE的斜率存在且不为零,可设DE的方程为x=my+a,
并设D(x1,y1),E(x2,y2).联立:
代入整理得y2-4my-4a=0从而有y1+y2=4m①,y1y2=-4a②
又k1k2=1?
•
=1,又y12=4x1,y22=4x2,∴k1k2=1?
•
=1
?
=1?(y1+2)(y2+2)=16,展开即得y1y2+2(y1+y2)-12=0
将①②代入得-4a+2×4m-12=0,即a=2m-3,得,DE:x=my+2m-3,
即(x+3)=m(y+2),故直线DE经过(-3,-2)这个定点.
| PN |
| NF |
| PN |
| 1 |
| 2 |
| NF |
| 1 |
| 2 |
| PN |
| 1 |
| 2 |
| NF |
| NF |
| 1 |
| 2 |
化简得y2=4x,即为所求的P点的轨迹C的对应的方程.
(2)由题意可知直线DE的斜率存在且不为零,可设DE的方程为x=my+a,
并设D(x1,y1),E(x2,y2).联立:
|
代入整理得y2-4my-4a=0从而有y1+y2=4m①,y1y2=-4a②
又k1k2=1?
| y1-2 |
| x1-1 |
| y2-2 |
| x2-1 |
| y1-2 | ||||
|
| y2-2 | ||||
|
?
| 16 |
| (y1+2)(y2+2) |
将①②代入得-4a+2×4m-12=0,即a=2m-3,得,DE:x=my+2m-3,
即(x+3)=m(y+2),故直线DE经过(-3,-2)这个定点.
点评:本题考查点的轨迹方程的求法和证明直线DE过定点,并求出这个定点.解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
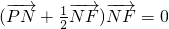
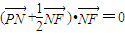 .
.