题目内容
已知F(1,0),P是平面上一动点,P到直线l:x=-1上的射影为点N,且满足(
+
)•
=0
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过点M(1,2)作曲线C的两条弦MA,MB,设MA,MB所在直线的斜率分别为k1,k2,当k1,k2变化且满足k1+k2=-1时,证明直线AB恒过定点,并求出该定点坐标.
| PN |
| 1 |
| 2 |
| NF |
| NF |
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过点M(1,2)作曲线C的两条弦MA,MB,设MA,MB所在直线的斜率分别为k1,k2,当k1,k2变化且满足k1+k2=-1时,证明直线AB恒过定点,并求出该定点坐标.
分析:(Ⅰ)设出动点P的坐标,求出N点的坐标,再求出向量
,
,然后代入(
+
)•
=0整理即可得到点P的轨迹C的方程;
(Ⅱ)设出点A,B的坐标,写出直线MA,MB的方程,和抛物线联立后利用根与系数关系求出A点和B点的纵坐标,然后求出两纵坐标的和与积,然后由直线方程的两点式写出AB的直线方程,把两纵坐标的和与积代入直线方程后,利用直线系方程的知识可求出直线AB经过的定点.
| PN |
| NF |
| PN |
| 1 |
| 2 |
| NF |
| NF |
(Ⅱ)设出点A,B的坐标,写出直线MA,MB的方程,和抛物线联立后利用根与系数关系求出A点和B点的纵坐标,然后求出两纵坐标的和与积,然后由直线方程的两点式写出AB的直线方程,把两纵坐标的和与积代入直线方程后,利用直线系方程的知识可求出直线AB经过的定点.
解答:解:(Ⅰ)设曲线C上任意一点P(x,y),又F(1,0),N(-1,y),
从而
=(-1-x,0),
=(2,-y),
则
+
=(-1-x,0)+
(2,-y)=(-x,-
y),
由(
+
)•
=0,得(-x,-
y)•(2,-y)=0,
即-2x+
y2=0.
化简得y2=4x,即为所求的P点的轨迹C的对应的方程.
(Ⅱ)设A(x1,y1)、B(x2,y2),
MA:y=k1(x-1)+2,
MB:y=k2(x-1)+2.
将y=k1(x-1)+2与y2=4x联立,得:k1y2-4y-4k1+8=0
由y1+2=
,得y1=
-2①
同理 y2=
-2②
而AB直线方程为:y-y1=
(x-x1),
即y=
x+
③
由①②:y1+y2=
-2+
-2=
-4=
-4
y1y2=4(
-
+1)=4(
+1)
代入③得,y=
x+
,
整理得k1k2(x+y+1)+6+y=0.
则
⇒
,故直线AB经过定点(5,-6).
从而
| PN |
| NF |
则
| PN |
| 1 |
| 2 |
| NF |
| 1 |
| 2 |
| 1 |
| 2 |
由(
| PN |
| 1 |
| 2 |
| NF |
| NF |
| 1 |
| 2 |
即-2x+
| 1 |
| 2 |
化简得y2=4x,即为所求的P点的轨迹C的对应的方程.
(Ⅱ)设A(x1,y1)、B(x2,y2),
MA:y=k1(x-1)+2,
MB:y=k2(x-1)+2.
将y=k1(x-1)+2与y2=4x联立,得:k1y2-4y-4k1+8=0
由y1+2=
| 4 |
| k1 |
| 4 |
| k1 |
同理 y2=
| 4 |
| k2 |
而AB直线方程为:y-y1=
| y2-y1 |
| x2-x1 |
即y=
| 4 |
| y1+y2 |
| y1y2 |
| y1+y2 |
由①②:y1+y2=
| 4 |
| k1 |
| 4 |
| k2 |
| 4(k1+k2) |
| k1k2 |
| -4 |
| k1k2 |
y1y2=4(
| 4 |
| k1k2 |
| 2(k1+k2) |
| k1k2 |
| 6 |
| k1k2 |
代入③得,y=
| 4 | ||
|
| ||
|
整理得k1k2(x+y+1)+6+y=0.
则
|
|
点评:本题考查了抛物线的方程,考查了直线与抛物线的综合,训练了一元二次方程的根与系数关系,考查了直线系方程,此题是有一定难度题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
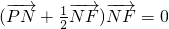
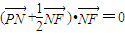 .
.