题目内容
已知椭圆方程为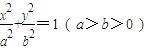 ,它的一个顶点为M(0,1),离心率
,它的一个顶点为M(0,1),离心率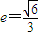 .
.(1)求椭圆的方程;
(2)设直线l与椭圆交于A,B两点,坐标原点O到直线l的距离为
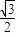 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
【答案】分析:(1)求椭圆的方程,它的一个顶点为M(0,1),离心率 .建立方程
.建立方程 求同a,b,即可得到椭圆的方程.
求同a,b,即可得到椭圆的方程.
(2)由于已知坐标原点O到直线l的距离为 ,故求△AOB面积的最大值的问题转化为求线段AB的最大值的问题,由弦长公式将其表示出来,再判断最值即可得到线段AB的最大值.
,故求△AOB面积的最大值的问题转化为求线段AB的最大值的问题,由弦长公式将其表示出来,再判断最值即可得到线段AB的最大值.
解答:解:(1)设 ,
,
依题意得 (2分)解得
(2分)解得 .(3分)∴椭圆的方程为
.(3分)∴椭圆的方程为 ..(4分)
..(4分)
(2)①当AB .(5分)
.(5分)
②当AB与x轴不垂直时,
设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
由已知 ,得
,得 ,..(6分)
,..(6分)
把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2-3=0,
∴ (7分)
(7分)
∴|AB|2=(1+k2)(x2-x1)2= =
= =
=
 .
.
当且仅当 时等号成立,此时|AB|=2.(10分)
时等号成立,此时|AB|=2.(10分)
③当 (11分)
(11分)
综上所述:|AB|max=2,
此时△AOB面积取最大值 (12分)
(12分)
点评:本题考查直线与圆锥曲线的综合问题,解答本题关键是对直线AB的位置关系进行讨论,可能的最值来,本题由于要联立方程求弦长,故运算量比较大,又都是符号运算,极易出错,做题时要严谨认真.利用弦长公式求弦长,规律固定,因此此类题难度降低不少,因为有此固定规律,方法易找,只是运算量较大.
 .建立方程
.建立方程 求同a,b,即可得到椭圆的方程.
求同a,b,即可得到椭圆的方程.(2)由于已知坐标原点O到直线l的距离为
 ,故求△AOB面积的最大值的问题转化为求线段AB的最大值的问题,由弦长公式将其表示出来,再判断最值即可得到线段AB的最大值.
,故求△AOB面积的最大值的问题转化为求线段AB的最大值的问题,由弦长公式将其表示出来,再判断最值即可得到线段AB的最大值.解答:解:(1)设
 ,
,依题意得
 (2分)解得
(2分)解得 .(3分)∴椭圆的方程为
.(3分)∴椭圆的方程为 ..(4分)
..(4分)(2)①当AB
 .(5分)
.(5分)②当AB与x轴不垂直时,
设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
由已知
 ,得
,得 ,..(6分)
,..(6分)把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2-3=0,
∴
 (7分)
(7分)∴|AB|2=(1+k2)(x2-x1)2=
 =
= =
=
 .
.当且仅当
 时等号成立,此时|AB|=2.(10分)
时等号成立,此时|AB|=2.(10分)③当
 (11分)
(11分)综上所述:|AB|max=2,
此时△AOB面积取最大值
 (12分)
(12分)点评:本题考查直线与圆锥曲线的综合问题,解答本题关键是对直线AB的位置关系进行讨论,可能的最值来,本题由于要联立方程求弦长,故运算量比较大,又都是符号运算,极易出错,做题时要严谨认真.利用弦长公式求弦长,规律固定,因此此类题难度降低不少,因为有此固定规律,方法易找,只是运算量较大.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
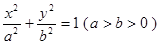 ,它的一个顶点为
,它的一个顶点为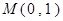 ,离心率
,离心率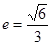 .
.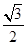 ,求△AOB面
,求△AOB面 .
.