题目内容
已知椭圆方程为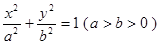 ,它的一个顶点为
,它的一个顶点为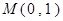 ,离心率
,离心率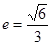 .
.
(1)求椭圆的方程;
(2)设直线l与椭圆交于A,B两点,坐标原点O到直线l的距离为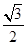 ,求△AOB面
,求△AOB面
积的最大值.
【答案】
(1) (2)
(2)
【解析】本试题主要是考查了椭圆方程的求解以及直线与椭圆位置关系的综合运用。
(1)设 ,
,
依题意得 ……2分 解得
……2分 解得 ,解得。
,解得。
(2)联立方程组,结合韦达定理和三角形的面积公式得到结论。
解:(1)设 ,
,
依题意得 ……2分 解得
……2分 解得 ….3分
….3分
 椭圆的方程为
椭圆的方程为 ….4分
….4分
(2)①当AB ……5分 ②当AB与
……5分 ②当AB与 轴不垂直时,
轴不垂直时,
设直线AB的方程为 ,
,
由已知 得
得 ………………………..6分
………………………..6分
 代入椭圆方程,整理得
代入椭圆方程,整理得 
 ………………….….7分
………………….….7分





当且仅当 时等号成立,此时
时等号成立,此时 ………10分
………10分
③当 …..11分 综上所述:
…..11分 综上所述: ,
,
此时 面积取最大值
面积取最大值 ……………..12分
……………..12分
有其它解答,请老师们参考评分标准酌情给分!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.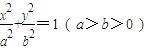 ,它的一个顶点为M(0,1),离心率
,它的一个顶点为M(0,1),离心率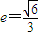 .
.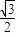 ,求△AOB面积的最大值.
,求△AOB面积的最大值.