题目内容
【题目】已知![]() ,
, ![]() 为抛物线
为抛物线![]() 上的两个动点,其中
上的两个动点,其中![]() ,且
,且![]()
(1)求证:线段![]() 的垂直平分线恒过定点
的垂直平分线恒过定点![]() ,并求出
,并求出![]() 点坐标;
点坐标;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)恒过定点![]() ;(2)
;(2)![]() 面积的最大值
面积的最大值![]() .
.
【解析】试题分析:(1)由抛物线的对称性可知定点![]() 一定在
一定在![]() 轴上,设
轴上,设![]() ,由
,由![]() ,可得
,可得![]() ,所以恒过定点
,所以恒过定点![]() ;(2)直线
;(2)直线![]() 方程:
方程: ![]() ,代入
,代入![]()
得![]() ,根据根据韦达定理,弦长公式将
,根据根据韦达定理,弦长公式将![]() 面积用
面积用![]() 表示,换元后,利用导数研究函数的单调性,从而可得结果.
表示,换元后,利用导数研究函数的单调性,从而可得结果.
试题解析:(1)由抛物线的对称性可知定点![]() 一定在
一定在![]() 轴上,设
轴上,设![]() ,
,
设![]() 中点为
中点为![]()
则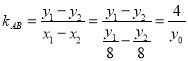 ,
, ![]()
由![]() ,可得
,可得![]() ,所以恒过定点
,所以恒过定点![]() ;
;
(2)直线![]() 方程:
方程: ![]() ,代入
,代入![]()
得![]()
由韦达定理知![]()
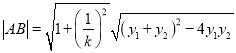
![]()
![]() 点到直线
点到直线![]() 的距离:
的距离: 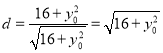
![]()
![]()
令![]() ,因为
,因为![]() ,所以
,所以![]()
则![]() ,
, ![]()
可知, ![]() ,
, ![]() ,
, ![]() 为增函数;
为增函数;
![]() ,
, ![]() ,
, ![]() 为减函数.
为减函数.
所以: ![]() ,
,
所以![]() 面积的最大值
面积的最大值![]() .
.
【方法点晴】本题主要考查抛物线的方程与性质及直线与抛物线的位置关系以及曲线过定点问题,属于难题.解决曲线过定点问题一般有两种方法:① 探索曲线过定点时,可设出曲线方程 ,然后利用条件建立等量关系进行消元,借助于曲线系的思想找出定点,或者利用方程恒成立列方程组求出定点坐标.② 从特殊情况入手,先探求定点,再证明与变量无关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
