题目内容
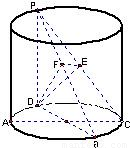
如图,PD是圆柱的母线,AC和BD是圆柱底面圆的互相垂直的两条直径,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F(1)求证:PB⊥平面EFD;(2)求二面角C-PB-D的大小.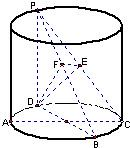

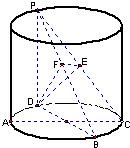
(1)因为PD是圆柱的母线,AC和BD是圆柱底面圆的互相垂直的两条直径,
所以PD⊥平面ABCD,PD⊥BC,四边形ABCD是正方形,BC⊥CD,
所以BC⊥平面PDC,又DE?平面PDC,
所以DE⊥BC,因为PD=DC,点E是PC的中点,所以DE⊥PC,
于是DE⊥平面PBC,有DE⊥PB,由EF⊥PB,EF∩DE=E,
得PB⊥平面EFD.
(2)由(1)知,PB⊥平面EFD,所以PB⊥DF,∠EFD是二面角C-PB-D的平面角,
设PD=DC=a,有DE=
| ||
| 2 |
在Rt△PDB中,DF=
| PD•DB |
| PB |
| ||
| 3 |
在Rt△PCB中,
| EF |
| BC |
| PE |
| PB |
得EF=
| ||
| 6 |
于是cos∠EFD=
| EF2+DF2-DE2 |
| 2EF•DF |
| 1 |
| 2 |
所以∠EFD=60°.于是二面角C-PB-D的大小为60°.

练习册系列答案
相关题目
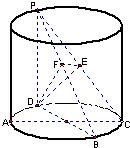 如图,PD是圆柱的母线,AC和BD是圆柱底面圆的互相垂直的两条直径,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F(1)求证:PB⊥平面EFD;(2)求二面角C-PB-D的大小.
如图,PD是圆柱的母线,AC和BD是圆柱底面圆的互相垂直的两条直径,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F(1)求证:PB⊥平面EFD;(2)求二面角C-PB-D的大小. (2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
(2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.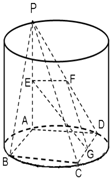 如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.