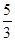题目内容
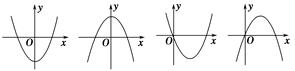
设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是 ( )
D
解析试题分析:经检验,A:若曲线为原函数图像,先减后增,则其导函数先负后正,正确;B:若一直上升的图像为原函数图像,单调递增,则其导函数始终为正,正确;C:若下方的图像为原函数,单调递增,则其导函数始终为正,正确;D:若下方的函数为原函数,则由其导函数为正,可知原函数应单调递增,矛盾,若上方的函数图像为原函数,则由其导函数可知,原函数应先减后增,矛盾,故选D.
考点:导数的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数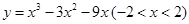 有( ).
有( ).
A.极大值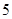 ,极小值 ,极小值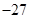 | B.极大值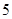 ,极小值 ,极小值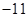 |
C.极大值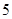 ,无极小值 ,无极小值 | D.极小值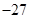 ,无极大值 ,无极大值 |
设曲线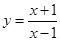 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则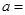
| A.2 | B.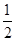 | C.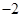 | D.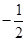 |
函数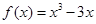 在区间
在区间 上( )
上( )
| A.有最大值,但无最小值 |
| B.有最大值,也有最小值 |
| C.无最大值,但有最小值 |
| D.既无最大值,也无最小值. |
函数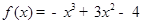 的单调递增区间是 ( )
的单调递增区间是 ( )
A.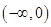 | B.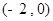 | C.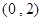 | D.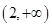 |
对任意实数 ,定义运算
,定义运算 :
: ,设
,设 ,则
,则 的值是( )
的值是( )
A. | B.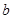 | C.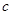 | D.不确定 |
由直线 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B.1 | C. | D. |
已知正四棱锥S—ABCD中,SA=2 ,那么当该棱锥的体积最大时,它的高为( )
,那么当该棱锥的体积最大时,它的高为( )
| A.1 | B. | C.2 | D.3 |
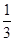 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )