题目内容
19.曲线$\left\{\begin{array}{l}x=cosθ\\ y=1+sinθ\end{array}\right.$(θ为参数)与直线x+y-1=0相交于A,B两点,则|AB|=2.分析 根据题意,将曲线的参数方程变形可得其普通方程,求出其圆心坐标及半径,分析可得圆心在直线上,则|AB|=2r,即可得答案.
解答 解:根据题意,曲线$\left\{\begin{array}{l}x=cosθ\\ y=1+sinθ\end{array}\right.$的普通方程为x2+(y-1)2=1,
圆心坐标为(0,1),半径r=1,
而直线的方程为x+y-1=0,圆心在直线上,
则AB为圆的直径,故|AB|=2r=2;
故答案为:2.
点评 本题考查圆的参数方程,涉及直线与圆的位置关系,关键是将圆的参数方程化为普通方程.

练习册系列答案
相关题目
10.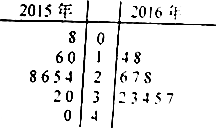 随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )
随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )
 随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )
随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )| A. | $\overline{X}$2015>$\overline{X}$2016,S22015>S22016 | B. | $\overline{X}$2015>$\overline{X}$2016,S22015<S22016 | ||
| C. | $\overline{X}$2015<$\overline{X}$2016,S22015<S22016 | D. | $\overline{X}$2015<$\overline{X}$2016,S22015>S22016 |
14.若实数a,b,c满足对任意实数x,y有3x+4y-5≤ax+by+c≤3x+4y+5,则( )
| A. | a+b-c的最小值为2 | B. | a-b+c的最小值为-4 | ||
| C. | a+b-c的最大值为4 | D. | a-b+c的最大值为6 |
1.已知函数f(x)=aex-x2-(3a+1)x,若函数f(x)在区间(0,ln3)上有极值,则实数a的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-1) | C. | (-1,-$\frac{1}{2}$) | D. | (-∞,-2)∪(0,1) |
5.函数f(x)=e-x的导数是( )
| A. | -e-x | B. | e-x | C. | -ex | D. | ex |