题目内容
一个球与一个正方体内切，已知这个球的体积是4| 3 |
分析：一个球与一个正方体内切，说明球的直径就是正方体的棱长，求出正方体的棱长，即可求正方体的体积．
解答：解：一个球与一个正方体内切，说明球的直径就是正方体的棱长，所以球的体积是4
π时，
正方体的棱长为：2r；
=4
π，解得r=
，正方体的棱长为：2
．
正方体的体积为：(2
)3=24
．
故答案为24
| 3 |
正方体的棱长为：2r；
| 4πr3 |
| 3 |
| 3 |
| 3 |
| 3 |
正方体的体积为：(2
| 3 |
| 3 |
故答案为24
| 3 |
点评：本题是基础题，考查正方体的内切球的知识，考查球的体积正方体的体积，计算能力，注意到球的直径就是正方体的棱长是本题的突破口．
练习册系列答案
教材全解字词句篇系列答案
相关题目
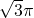，则这个正方体的体积是 ________．
，则这个正方体的体积是 . 
，则这个正方体的体积是 ．