题目内容
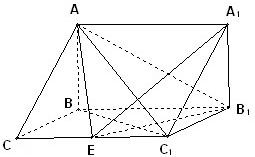
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=2,AB= , ∠BCC1=
, ∠BCC1=  。
。
(1)求证:C1B⊥平面ABC;
(2)当E为CC1的中点时,求二面角A-EB1-A1的平面角的正切值。
 , ∠BCC1=
, ∠BCC1=  。
。(1)求证:C1B⊥平面ABC;
(2)当E为CC1的中点时,求二面角A-EB1-A1的平面角的正切值。

证(1)因为AB⊥侧面BB1C1C,故AB⊥BC1
在△BC1C中,BC=1,CC1=BB1=2, ∠BCC1=
由余弦定理有

故有 BC2+BC12=CC12
∴C1B⊥BC
而BC∩AB=B 且AB,BC 平面ABC
平面ABC
∴C1B⊥平面ABC
(2)取EB1的中点D,A1E的中点F,BB1的中点N,AB1的中点M,
连DF则DF∥A1B1,连DN则DN∥BE,连MN则MN∥A1B1
连MF则MF∥BE,且MNDF为矩形,MD∥AE
又∵A1B1⊥EB1,BE⊥EB1
故∠MDF为所求二面角的平面角
在Rt△DFM中,DF= A1B1=
A1B1=  (∵△BCE为正三角形)
(∵△BCE为正三角形)

∴tan∠MDF=

在△BC1C中,BC=1,CC1=BB1=2, ∠BCC1=

由余弦定理有

故有 BC2+BC12=CC12
∴C1B⊥BC
而BC∩AB=B 且AB,BC
 平面ABC
平面ABC ∴C1B⊥平面ABC
(2)取EB1的中点D,A1E的中点F,BB1的中点N,AB1的中点M,
连DF则DF∥A1B1,连DN则DN∥BE,连MN则MN∥A1B1
连MF则MF∥BE,且MNDF为矩形,MD∥AE
又∵A1B1⊥EB1,BE⊥EB1
故∠MDF为所求二面角的平面角
在Rt△DFM中,DF=
 A1B1=
A1B1=  (∵△BCE为正三角形)
(∵△BCE为正三角形) 
∴tan∠MDF=



练习册系列答案
相关题目
 如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=C1C,∠BCC1=
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=C1C,∠BCC1=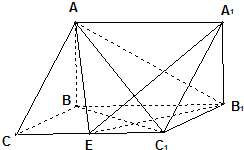 如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知 如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知
 ,求二面角A-EB1-A1的平面角的正切值.
,求二面角A-EB1-A1的平面角的正切值.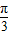 ,
,