Question

【题目】已知函数，．

（1）当时，

①若曲线与直线相切，求c的值；

②若曲线与直线有公共点，求c的取值范围．

（2）当时，不等式对于任意正实数x恒成立，当c取得最大值时，求a，b的值．

Answer 1

【答案】（1）,（2），．

【解析】

（1）当时，，所以，①设切点为，列出方程组，即可求得，得到答案； ②由题意，得方程有正实数根，即方程有正实数根，记，利用导数求得函数的单调性与最小值，即可求解的取值范围；

（2）由题意得，当时，对于任意正实数恒成立，即当时，对于任意正实数恒成立， 由（1）可得，进而得到，

，得到时，，进而得到 对于任意正实数恒成立，再利用二次函数的性质，即可得到结论.

（1）解：当时，，所以．

①设切点为，则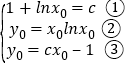

由②③得，

由①得代入④得，

所以．

②由题意，得方程有正实数根，

即方程有正实数根，

记，令，

当时，；当时，；

所以在上为减函数，在上为增函数；

所以．

若，则，不合；

若，由①知适合；

若，则，又，

所以，由零点存在性定理知在上必有零点．

综上，c的取值范围为．

（2）由题意得，当时，对于任意正实数x恒成立，

所以当时，对于任意正实数x恒成立，

由（1）知，，

两边同时乘以x得，①，

两边同时加上得，②，

所以（*），当且仅当时取等号．

对（*）式重复以上步骤①②可得，，

进而可得，，，……，

所以当，时，，当且仅当时取等号．

所以．

当取最大值1时，对于任意正实数x恒成立，

令上式中得， ，所以，

所以对于任意正实数x恒成立，

即对于任意正实数x恒成立，

所以，所以函数的对称轴，

所以，即，所以，．

又由，两边同乘以x2得，，

所以当，时，也恒成立，

综上，得，．