题目内容
13.如果关于x的不等式|x-2|-|x-5|<2的解集为{x|x<$\frac{9}{2}$}.分析 通过讨论x的范围,求出各个区间上的x的范围,取并集即可.
解答 解:令f(x)=|x-2|-|x-5|=$\left\{\begin{array}{l}{3,x≥5}\\{2x-7,2≤x<5}\\{-3,x<2}\end{array}\right.$,
故x≥5时,不和题意,
2≤x<5,解不等式2x-7<2,解得:2≤x<$\frac{9}{2}$,
x<2时,-3<2,符合题意,
故不等式的解集是{x|x<$\frac{9}{2}$},
故答案为:{x|x<$\frac{9}{2}$}.
点评 本题考查了绝对值不等式的解法,考查分类讨论思想,是一道基础题.

练习册系列答案
相关题目
13.若命题“存在x0∈R,使得mx02+mx0+2≤0”为假命题,则实数m的取值范围是( )
| A. | (-∞,0]∪[8,+∞) | B. | (0,8] | C. | [0,8) | D. | (0,8) |
8.抛掷一个均匀的正方体玩具(它的每一面上分别标有数字1,2,3,4,5,6),它落地时向上的数是3的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
3.某食品安检部门调查一个养殖场的养殖鱼的有关情况,安检人员从这个养殖场中不同位置共捕捞出100条鱼,称得每条鱼的重量(单位:千克),并将所得数据进行统计得如表.
若规定重量大于或等于1.20kg的鱼占捕捞鱼总量的15%以上时,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
(1)根据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否有问题?
(2)上面所捕捞的100条鱼中,从重量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得鱼的重量在[1.00,1.05)和[1,.25,1.30)中各有1条的概率.
| 鱼的重量 | [1.00,1.05) | [1.05,1.10) | [1.10,1.15) | [1.15,1.20) | [1.20,1.25) | [1.25,1.30) |
| 鱼的条数 | 3 | 20 | 35 | 31 | 9 | 2 |
(1)根据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否有问题?
(2)上面所捕捞的100条鱼中,从重量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得鱼的重量在[1.00,1.05)和[1,.25,1.30)中各有1条的概率.
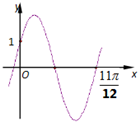 已知函数f(x)=2sin(ωx+ϕ)(ω>0,|ϕ|<$\frac{π}{2}$)的图象如图所示,则函数f(x)的解析式是f(x)=2sin(2x+$\frac{π}{6}$).
已知函数f(x)=2sin(ωx+ϕ)(ω>0,|ϕ|<$\frac{π}{2}$)的图象如图所示,则函数f(x)的解析式是f(x)=2sin(2x+$\frac{π}{6}$).