题目内容
19.判断函数y=$\frac{{a}^{x}-1}{{a}^{x}+1}+ln\frac{{a}^{x}-1}{{a}^{x}+1}$的奇偶性.分析 确定函数的定义域不关于原点对称,即可得出结论.
解答 解:由$\frac{{a}^{x}-1}{{a}^{x}+1}$>0,可得a>1时,x>0;0<a<1时,x<0,
定义域不关于原点对称,故非奇非偶.
点评 本题考查函数奇偶性,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
10.已知sin(π-α)=-$\frac{2}{5}$,且α是第四象限角,则tanα=( )
| A. | $\frac{2\sqrt{21}}{21}$ | B. | -$\frac{2\sqrt{21}}{21}$ | C. | -$\frac{2}{3}$ | D. | $\frac{\sqrt{21}}{2}$ |
14.在空间直角坐标系Oxy中,$\overrightarrow{AB}=-\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}-3\overrightarrow{{e}_{3}}$($\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}},\overrightarrow{{e}_{3}}$)分别是与x轴、y轴、z轴的正方向同向的单位向量),则点B的坐标为( )
| A. | (-$\overrightarrow{{e}_{1}},2\overrightarrow{{e}_{2}},-3\overrightarrow{{e}_{3}}$) | B. | (-1,2,-3) | C. | (1,-2,3) | D. | 不能确定 |
8.函数f(x)=x2-4x-lnx+4的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
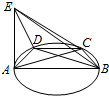 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).