题目内容
已知f（x）的图象在[a，b]上连续，则“f（a）•f（b）＜0”是“f（x）在（a，b）内有零点”的（ ）条件．
| A．充分不必要 | B．必要不充分 |
| C．充要 | D．既不充分也不必要 |
f（x）的图象在[a，b]上连续，只要满足f（a）•f（b）＜0，必有“f（x）在（a，b）内有零点”；
而“f（x）在（a，b）内有零点”，不能推出f（a）•f（b）＜0，比如函数f（x）=x2，
在区间（-1，1）上有零点0，但f（-1）•f（1）=1＞0，
故“f（a）•f（b）＜0”是“f（x）在（a，b）内有零点”的充分不必要条件，
故选A
而“f（x）在（a，b）内有零点”，不能推出f（a）•f（b）＜0，比如函数f（x）=x2，
在区间（-1，1）上有零点0，但f（-1）•f（1）=1＞0，
故“f（a）•f（b）＜0”是“f（x）在（a，b）内有零点”的充分不必要条件，
故选A
练习册系列答案
相关题目
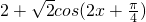的图象向左平移m个单位（m＞0），得到的图象关于直线
对称．