题目内容
 如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤
如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤ )的图象与y轴交与点(0,1).
)的图象与y轴交与点(0,1).
(1)求φ的值;
(2)设P是图象上的最高点,M,N是图象与x轴交点,求 夹角的余弦值.
夹角的余弦值.
解:(1)把点(0,1)代入函数y=2sin(πx+φ)可得,sinφ= ,再由0<φ≤
,再由0<φ≤ 知φ=
知φ= .
.
(2)由(1)知 函数y=2sin(πx+ ),结合图象可得点P(
),结合图象可得点P( ,2 ),
,2 ),
M(- ,0),N (
,0),N ( ,0),故PM=
,0),故PM= =
=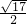 ,PN=
,PN= =
=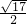 ,MN=1,
,MN=1,
△PMN中,由余弦定理可得 1= +
+ -2×
-2×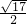 ×
×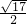 cos<
cos< >,
>,
解得 cos< >=
>=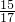 .
.
分析:(1)把点(0,1)代入函数y=2sin(πx+φ),再由∅的取值范围求出φ的值.
(2)由(1)知 函数y=2sin(πx+ ),结合图象可得点P(
),结合图象可得点P( ,2 ),M(-
,2 ),M(- ,0),N (
,0),N ( ,0),△PMN中,由余弦定理可求得cos<
,0),△PMN中,由余弦定理可求得cos< >的值.
>的值.
点评:本题主要考查余弦定理的应用,两个向量的数量积的定义,以及由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.
 ,再由0<φ≤
,再由0<φ≤ 知φ=
知φ= .
.(2)由(1)知 函数y=2sin(πx+
 ),结合图象可得点P(
),结合图象可得点P( ,2 ),
,2 ),M(-
 ,0),N (
,0),N ( ,0),故PM=
,0),故PM= =
=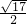 ,PN=
,PN= =
=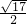 ,MN=1,
,MN=1,△PMN中,由余弦定理可得 1=
 +
+ -2×
-2×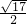 ×
×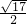 cos<
cos< >,
>,解得 cos<
 >=
>=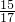 .
.分析:(1)把点(0,1)代入函数y=2sin(πx+φ),再由∅的取值范围求出φ的值.
(2)由(1)知 函数y=2sin(πx+
 ),结合图象可得点P(
),结合图象可得点P( ,2 ),M(-
,2 ),M(- ,0),N (
,0),N ( ,0),△PMN中,由余弦定理可求得cos<
,0),△PMN中,由余弦定理可求得cos< >的值.
>的值.点评:本题主要考查余弦定理的应用,两个向量的数量积的定义,以及由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目
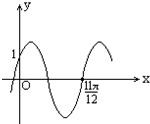
已知如图是函数y=2sin(ωx+φ)(|φ|<
)的图象,那么( )
| π |
| 2 |

A、?=
| ||||
B、?=
| ||||
C、?=2,φ=
| ||||
D、?=2,φ=-
|
 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ 已知如图是函数y=2sin(ωx+φ)(|φ|<
已知如图是函数y=2sin(ωx+φ)(|φ|< 如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤
如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤ 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤