题目内容
等差数列 的前
的前 项的和为
项的和为 ,且
,且 ,则
,则 ( )
( )
 的前
的前 项的和为
项的和为 ,且
,且 ,则
,则 ( )
( )| A. 2012 | B.2012 | C. 2011 | D.2011 |
D
试题分析:根据题意可知,由于等差数列
 的前
的前 项的和为
项的和为 ,且
,且 则说明
则说明
同时结合
 ,可知其首项为2011,故选D.
,可知其首项为2011,故选D.点评:等差数列的通项公式和前n项和的关系式是解决该试题的关键,属于基础题。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
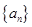 的前
的前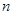 项和
项和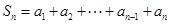 ,求证:
,求证: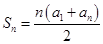
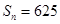 ,求
,求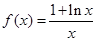 .
.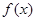 在区间
在区间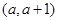 上有极值,求实数
上有极值,求实数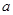 的取值范围;
的取值范围;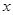 的方程
的方程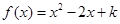 有实数解,求实数
有实数解,求实数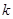 的取值范围;
的取值范围;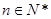 ,
,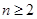 时,求证:
时,求证: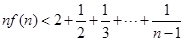 .
. 中,前
中,前 项和为
项和为 ,且
,且 .
. ,求数列
,求数列 前
前 .
. 满足
满足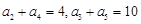 ,则它的前10项和
,则它的前10项和 ______
______  ,
, ,
, ,则
,则 的值为( )。
的值为( )。 满足
满足 ,
,
 ,则此数列的通项
,则此数列的通项 等于( )
等于( )


 }中,
}中, =2,
=2, =7,则
=7,则 =
=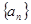 的相邻两项
的相邻两项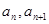 是关于
是关于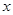 的方程
的方程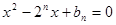
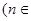 N
N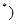 的两根,且
的两根,且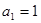 .
.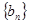 的通项公式;
的通项公式;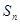 是数列
是数列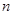 项和, 问是否存在常数
项和, 问是否存在常数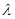 ,使得
,使得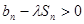 对任意
对任意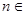 N
N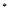 都成立,若存在, 求出
都成立,若存在, 求出